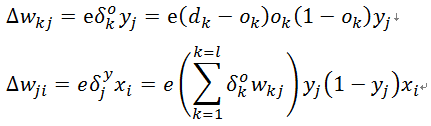人工神经网络

人工神经网络（Artificial Neural Network，即ANN），是20世纪80年代以来人工智能领域兴起的研究热点。它从信息处理角度对人脑神经元网络进行抽象建立某种简单模型，按照不同的连接方式组成不同的网络。神经网络使用运算模型，由大量的节点（或称神经元或感知器）之间相互连接构成。每个节点代表一种特定的输出函数，称为激励函数（activation function）。每两个节点间的连接都代表一个对于通过该连接信号的加权值，称之为权重，这相当于人工神经网络的记忆。

多层网络可以解决单层网络所无法解决的问题，如非线性分类、精度极高的函数逼近等，只要有足够多的神经元，这些都可以实现。人工神经网络一般作为分类器来使用，是有监督学习方法。

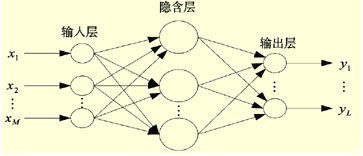
常见的人工神经网络一般简单地分为三层：输入层，隐层和输出层：

BP反向传播算法

感知器可以通过梯度下降法来进行训练，多层人工神经网络可以通过相似的方法来处理，也就是所说的BP反向传播算法，经典的BP网络其具体结构如：

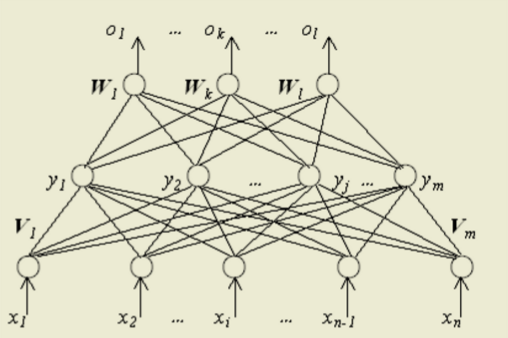
输入层一共n个节点：

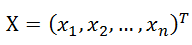
网络的输入信号是一个n维向量，与学习样本的n维特征相对应。学习算法的每一次迭代处理，直接把样本的每一个分量赋给输入节点。

隐层一共m个节点：

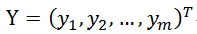
输入节点与隐层之间的权值矩阵记作V，这里，隐层有m个神经元节点。所以，其有m个分量，每一个分量与所有输入层n个节点相连接，故而，m个分量中的每一个是分量是一个n维向量。即V是一个mxn的矩阵。

输出层一共l个节点：

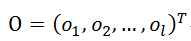
隐层与输出层之间的权值矩阵记作W。这里网络输出层有l个神经节点，所以一共有l个分量，每一个分量与所有隐层中的m个节点相连，故而，l中的每一个分量是一个m维向量。即W是一个lxm的矩阵。

期望输出：

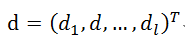
输入层到隐层的计算如下式（1）：

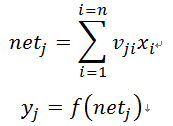
其中j=1,2…..,m。

隐层到输出层的计算如下式（2）：

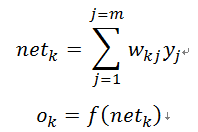
其中k=1,2…..,l。

网络输出层误差函数定义为式（3）：

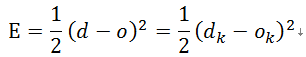
根据前面公式（1）和（2），将误差函数展开到隐层为式（4）：

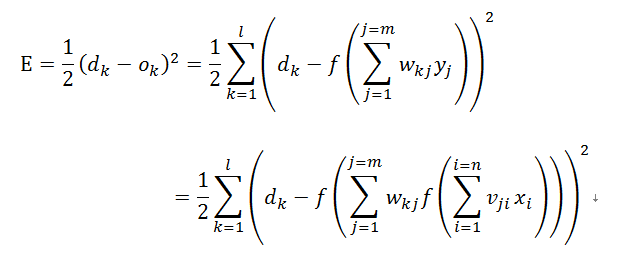
根据梯度下降策略，目的是求解误差关于各个权值的梯度，即权值迭代更新如下式（5）和（6）：

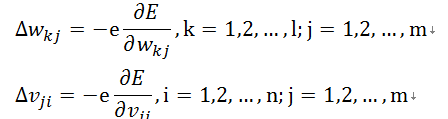
式中负号表示梯度下降，常数e属于区间（0,1），表示比例系数。为了方便记忆和书写，我们引入新的记号，这种记号在网络层数更多的时候有更方便地递归表达式。

先定义这样一个误差信号，对于输出层式（7）：

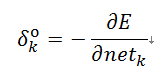
对于隐层式（8）：

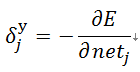
则上面的式（5）可以写成式（9）：

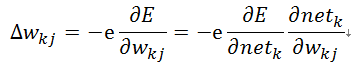
上面的式（6）可以写成式（10）：

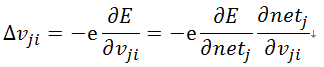
然后式（9）可以简单表示为式（11）：

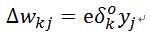
然后式（10）可以简单表示为式（12）：

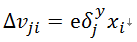
下面进一步计算定义的delta信号：

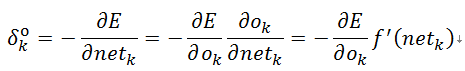
根据：

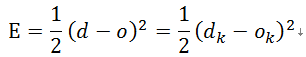
求导可得：

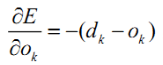
最后代入可得式（13）：

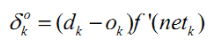
对于隐层：

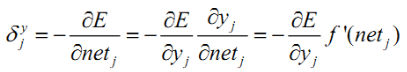
根据：

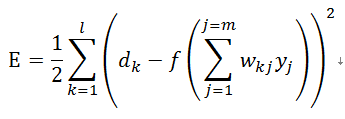
可得：

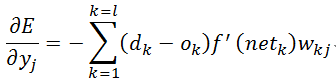
最后代入可得式（14）：

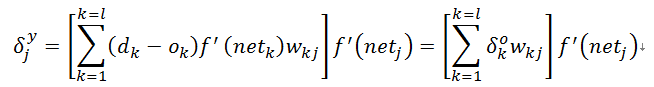
为了得到更为复杂的决策区域，我们采用某种非线性激励函数作用于单元的净输入，然后以非线性激励的响应（激励函数的输出）作为神经元的输出。非线性函数采用sigmoid函数：

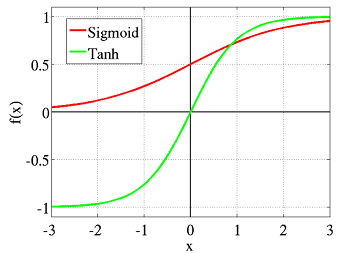
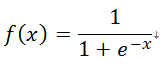
其导数数为：

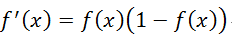
最终得到梯度更新变量：