最长公共子序列（LCS）和最长公共子串问题

什么是最长公共子序列

一个数列S，若分别是两个或多个已知序列的子序列，且是所有符合条件序列中最长的，则S称为已知序列的最长公共子序列。

例如：有两个随机数列，1 2 3 4 5 6 和 3 4 5 8 9，则它们的最长公共子序列便是：3 4 5。

最长公共子串和最长公共子序列的区别

最长公共子串（Longest Common Substirng）和最长公共子序列（Longest Common Subsequence，LCS）的区别为：子串是串的一个连续的部分，子序列则是从不改变序列的顺序，而从序列中去掉任意的元素而获得新的序列；也就是说，子串中字符的位置必须是连续的，子序列则可以不必连续。

蛮力法求最长公共子序列

蛮力法是解决最长公共子序列问题最容易想到的方法，即对S的每一个子序列，检查是否为T的子序列，从而确定它是否为S和T的公共子序列，并且选出最长的公共子序列。

S和T的所有子序列都检查过后即可求出S和T的最长公共子序列。S的一个子序列相应于下标序列1，2，…，n的一个子序列。因此，S共有2^n个子序列。当然，T也有2^m个子序列。因此，蛮力法的时间复杂度为O(2^n * 2^m)，这是指数级别，时间复杂度相当高。

动态规划方法

有序列str1和序列str2，长度分别为m和n，创建1个二维数组L[m+1][n+1]：

1、初始化L数组内容为0；

2、m和n分别从1开始，m++，n++循环：

如果str1[m] == str2[n]，则L[m,n] = L[m - 1][n -1] + 1；

如果str1[m] != str2[n]，则L[m,n] = max{L[m][n - 1]，L[m - 1[[n]}；

最后从L[m][n]中的数字一定是最大的，且这个数字就是最长公共子序列的长度，从数组L中找出一个最长的公共子序列。

从数组L中查找一个最长的公共子序列：

i和j分别从m，n开始，递减循环直到i = 0，j = 0。其中，m和n分别为两个串的长度。

如果str1[i] == str2[j]，则将str[i]字符插入到子序列内，i–，j–；

如果str1[i] != str[j]，则比较L[i][j-1]与L[i-1][j]，L[i][j-1]大，则j–，否则i–；（如果相等，则任选一个）

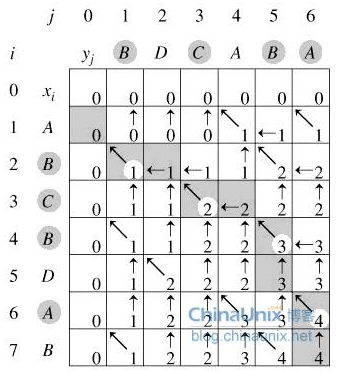
根据上图，我们可以得到其中公共子串：B C B A 和 B D A B。

代码实现：

#include <iostream>
#include <vector>
#include <string>
using namespace std;

int LCS(string s1,string s2){
	int len1=s1.size();
	int len2=s2.size();
	int *a=new int[len1+1];
	for(int i=0;i<=len1;i++)
		a[i]=0;
	vector<vector<int> > vec;
	for(int i=0;i<=len2;i++){
		vector<int> arr(a,a+len1+1);
		vec.push_back(arr);
	}
	for(int i=1;i<=len2;i++){
		for(int j=1;j<=len1;j++){
			if(s1[j-1]==s2[i-1]){
				vec[i][j]=vec[i-1][j-1]+1;
			}else{
				if(vec[i-1][j]>vec[i][j-1])
					vec[i][j]=vec[i-1][j];
				else
					vec[i][j]=vec[i][j-1];
			}
		}
	}
	return vec[len2][len1];
}

int main(){
	string str1="BDCABA";
	string str2="ABCBDAB";
	cout<<LCS(str1,str2)<<endl;
	system("pause");
}

最长公共子串

其实这是一个序贯决策问题，可以用动态规划来求解。我们采用一个二维矩阵来记录中间的结果。这个二维矩阵怎么构造呢？直接举个例子吧：”bab”和”caba”(当然我们现在一眼就可以看出来最长公共子串是”ba”或”ab”)

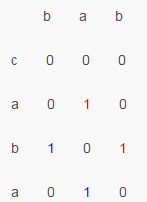
我们看矩阵的斜对角线最长的那个就能找出最长公共子串。

不过在二维矩阵上找最长的由1组成的斜对角线也是件麻烦费时的事，下面改进：当要在矩阵是填1时让它等于其左上角元素加1。

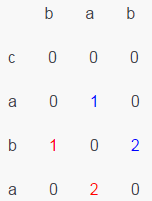
这样矩阵中的最大元素就是最长公共子串的长度。

在构造这个二维矩阵的过程中由于得出矩阵的某一行后其上一行就没用了，所以实际上在程序中可以用一维数组来代替这个矩阵。

Aris