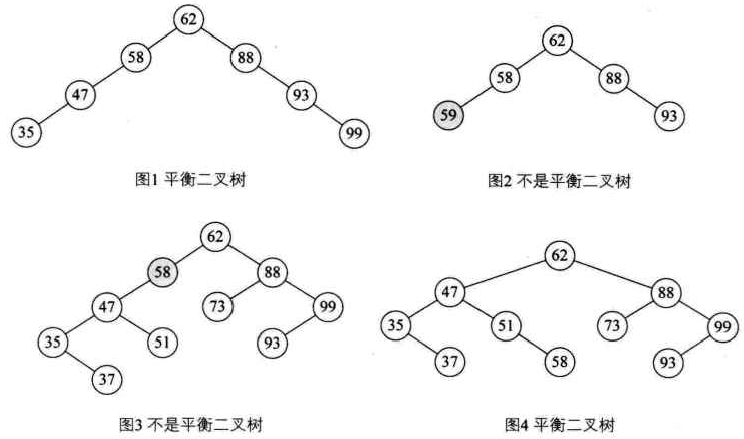
平衡二叉树的定义

平衡二叉树是一种二叉排序树，其中每个结点的左子树和右子树的高度差至多等于1，是一种高度平衡的二叉排序树。

我们将二叉树上结点的左子树深度减去右子树深度的值称为平衡因子BF，那么平衡二叉树上所有结点的平衡因子只可能是-1、0和1。只要二叉树上有一个结点的平衡因子绝对值大于1，则该二叉树就是不平衡。

关于平衡二叉树的定义理解，它的前提首先是一棵二叉排序树。如下图中的右上图的59比58大，却是58的左子树，这不符合二叉排序树的定义。图3不是平衡二叉树的原因就在于，结点58的左子树高度为2，而右子树为空，二者差大于绝对值1，因此是不平衡的。

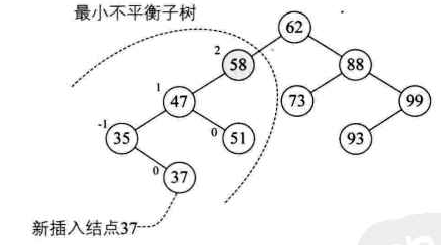
距离插入结点最近的，且平衡因子的绝对值大于1的结点为根的子树，我们称为最小不平衡子树。如下图，当新插入结点37时，距离它最近的平衡因子绝对值查过1的结点是58（即它的左子树高度2减去右子树高度0），所以从58开始以下的子树为最小不平衡子树。

平衡二叉树实现原理

平衡二叉树构建的基本思想就是构建二叉排序树的过程中，每当插入一个结点时，先检查是否因插入而破坏树的平衡性，若是，则找出最小不平衡子树。在保持二叉排序树特性的前提下，调整最小不平衡子树中各结点之间的链接关系，进行相应的旋转，使之成为新的平衡子树。

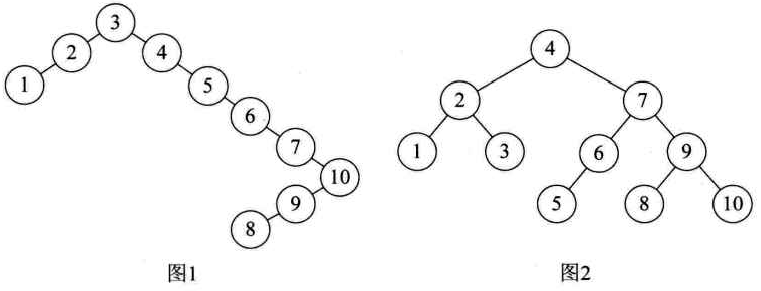
假设我们现在有一个数组a[10]={3,2,1,4,5,6,7,10,9,8}，根据二叉排序树的特性，我们通常会将它构建成如图1所示的样子。虽然它完全符合二叉排序树的定义，但是这样高度达到8的二叉树来说，查找是非常不利的。我们更期望能够构建成如图2的样子，高度为4的二叉排序树才可以提供高效的查找效率。

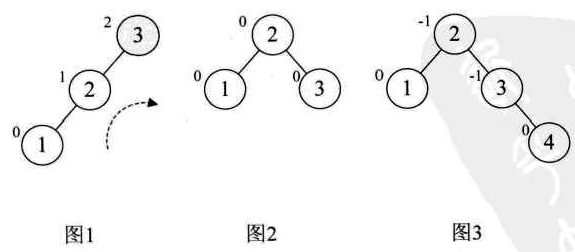
对于数组a的前两位3和2，我们很正常地构建，到了第3个数1时，发现此时根结点3的平衡因子变成2，此时整棵树都成了最小不平衡子树，因此需要调整。如下图1（结点左上角数字为平衡因子BF值）。因为BF值为正，因此我们将整个树进行右旋（顺时针旋转），此时结点2成了根结点，3成了2的右孩子，这样三个结点的BF值均为0，非常的平衡，如下图2所示。

然后我们再增加结点4，平衡因子没有发生改变，如图3。增加结点5时，结点3的BF值为-2，说明要旋转。由于BF为负值，所以我们对这颗最小平衡子树进行左旋（逆时针旋转），此时我们整颗树又达到了平衡。

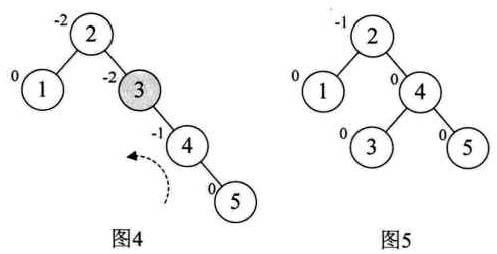
继续增加结点6时，发现根结点2的BF值变成了-2，如图6所示，所以我们对根结点进行了左旋，注意此时本来结点3和是结点4的左孩子，由于旋转后需要满足二叉排序树的特性，因此它就成了结点2的右孩子，如图7所示。增加结点7，同样的左旋转，使得整棵树达到平衡，如图8和图9所示。

当增加结点10时，结构无变化，如图10所示。再增加结点9，此时结点7的BF变成了-2，理论上我们只需要旋转最小不平衡子树7、9、10即可，但是如果左旋转后，结点9变成10的右孩子，这是不符合二叉排序树的特性的，此时不能做简单的左旋，如图11所示。

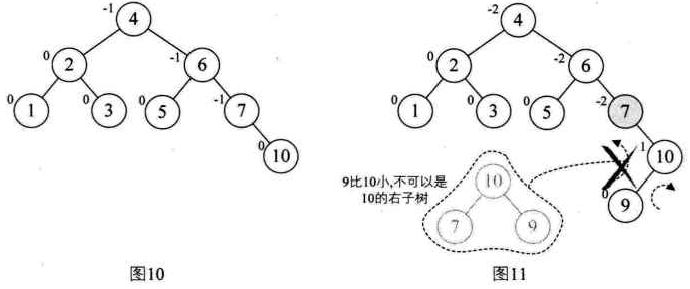
我们可以发现根本原因在于结点7的BF是-2，而结点10的BF是1，也就是说它们俩一正一负，符号并不统一，而前面的几次旋转，无论左旋还是右旋，最小不平衡子树的根结点与它的子结点符号都是相同的，这就是不能直接旋转的关键。

因此我们先把它们旋转到符号统一再说，于是先对结点9和结点10进行右旋，使得结点10成了9的右子树，结点9的BF为-1，此时就与结点7的BF值符号统一了，如图12所示。

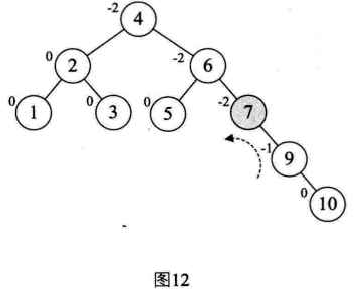
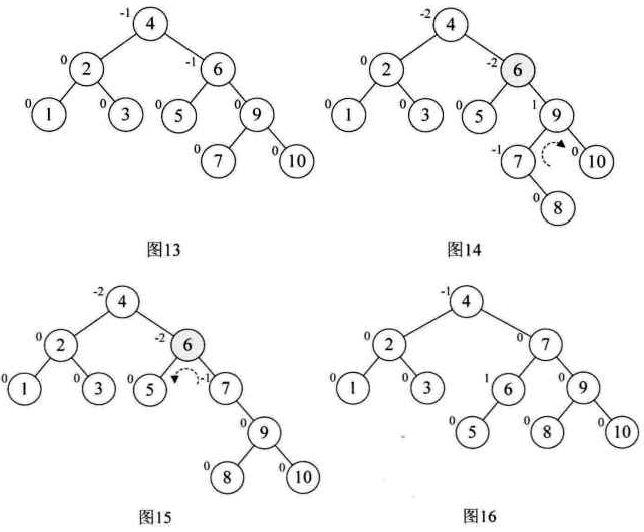
这样我们再以结点7为最小不平衡子树进行左旋，如图13，接着插入8，情况与刚才类似，结点6的BF是-2，而它的右孩子9的BF是1，如图14，因此首先以9为根结点，进行右旋，得到图15，此时结点6和结点7的符号都是负，在以6为根结点左旋，最终得到最后的平衡二叉树，如图16所示。

平衡二叉树总结

如果我们需要查找的集合本身没有顺序，在频繁查找的同时也需要经常的插入和删除操作，显然我们需要构建一颗二叉排序树，但是不平衡的二叉排序树的查找效率是非常低的，因此我们需要在构建的时候，就让这颗二叉排序树是平衡二叉树，此时我们的查找时间复杂度就为O(logn)（因为完全二叉树的深度为[log2n]+1），而插入和删除也为O(logn)（因为插入和删除需要查找位置，修改的复杂度为O(1)），这显然是比较理想的一种动态查找表算法。

有四种种情况可能导致二叉查找树不平衡，分别为：

（1）LL：插入一个新节点到根节点的左子树（Left）的左子树（Left），导致根节点的平衡因子由1变为2

（2）RR：插入一个新节点到根节点的右子树（Right）的右子树（Right），导致根节点的平衡因子由-1变为-2

（3）LR：插入一个新节点到根节点的左子树（Left）的右子树（Right），导致根节点的平衡因子由1变为2

（4）RL：插入一个新节点到根节点的右子树（Right）的左子树（Left），导致根节点的平衡因子由-1变为-2