二叉排序树的定义

二叉排序树是一种既可以保证插入和删除效率，又可以比较高效率地实现查找的算法。

假设我们的数据集开始只有一个数{62}，然后现在需要将88插入数据集，于是数据集成了{62,82}，还保持着从小到大有序。再查找有没有58，没有则插入，可此时要想在线性表的顺序存储中有序，就得移动62和88的位置。

可不可以不移动呢？当然是可以的，就是二叉树结构。当我们用二叉树的方式时，首先我们将第一个数62定为根结点，88因为比62大，因此让它做62的右子树，58因为比62小，所以成为它的左子树。此时58插入并没有影响到62和88的关系。

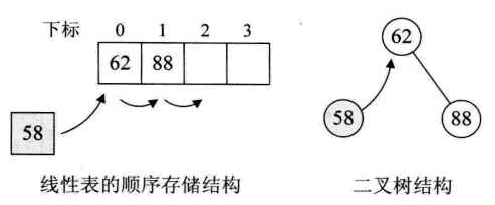
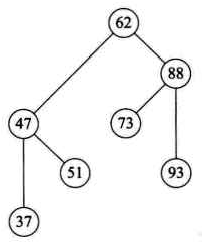
若我们现在需要对集合{62,88,58,47,35,73,51,99,37,93}做查找，使用排好序的二叉树来创建。

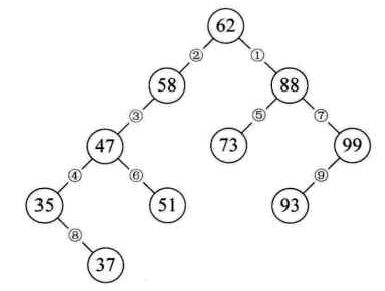
这样我们就得到了一颗二叉树，并且当我们对它进行中序遍历时，就可以得到一个有序的序列{35,37,47,51,58,62,73,88,93,99}。

二叉排序树，又称为二叉查找树，二元查找树。它或者是一棵空树，或者是具有下列性质的二叉树。

若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；

若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；

它的左、右子树也分别为二叉树排序树。

二叉排序树的查找

构造一颗二叉排序树的目的，并不是为了排序，而是为了提高查找和插入删除关键字的速度。

比如要查找93，过程如下：

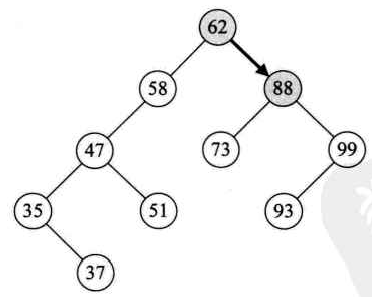
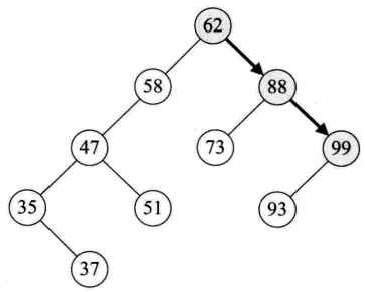
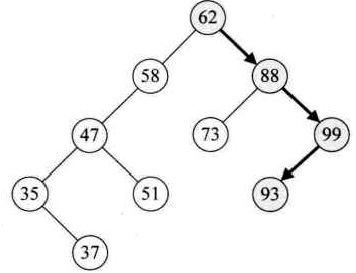
二叉排序树的插入

比如插入95：

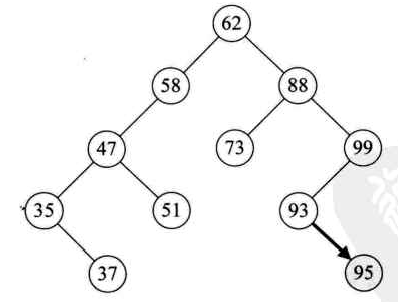
二叉排序树的删除

我们不能因为删除了结点而让这棵树变得不满足二叉排序树的特性，所以删除需要考虑多种情况。

如果需要查找并删除如37、51、73、93这些在二叉排序树中是叶子的结点，那是很容易的，毕竟删除它们对整颗树来说，其他结点的结构并未收到影响，如图所示：

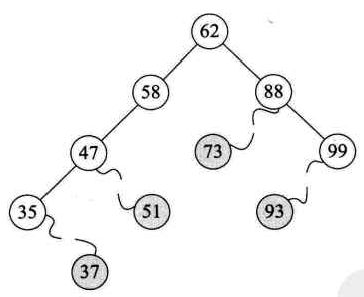
对应要删除的结点只有左子树或只有右子树的情况，相对也比较好解决。那就是结点删除后，将它的左子树或右子树整个移动到删除结点的位置即可，可以理解为独子继承父业。如图所示，先删除35和99结点，再删除58结点的变化图，最终，整个结构还是一个二叉排序树。

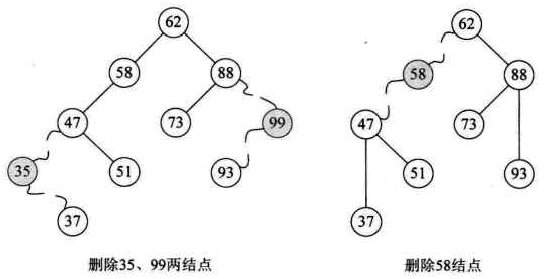
但是对于要删除的结点既有左子树又有右子树的情况怎么办呢？

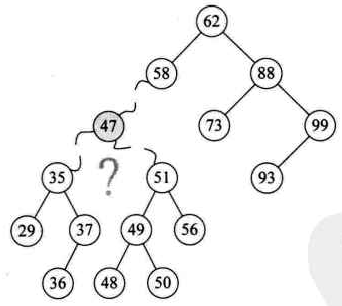
最初的想法是：我们当47结点只有一个左子树，做法就和一个左子树的操作一样，让35及它之下的结点成为58的左子树，然后再对47的右子树所有结点进行插入操作。这是比较简单的想法，可是47的右子树有子孙共5个结点，这么做效率不高且不说，还会导致整个二叉排序树结构发生很大的变化，有可能会增加树的高度，增加高度可不是好事。

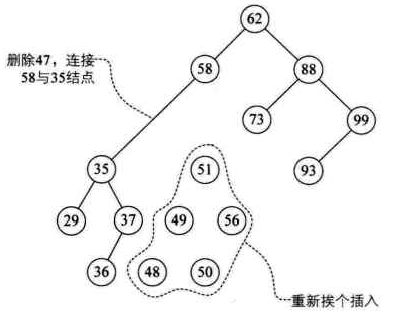
那么47的两个子树中能否找到一个结点可以替代47？有，37或者48都可以替代47，此时在删除47后，整个二叉排序树并没有发生什么本质的改变。

为什么是37和38呢？因为它们正好是二叉排序树中比它小或比它大的最接近47的两个数。如果我们对这颗二叉排序数进行中序遍历，得到的序列为{29,35,36,47,48,49,50,51,56,62,73,88,93,99}，它们正好是47的前驱和后继。

因此最好的办法是找到需要删除的结点p的直接前驱（或直接后继）s，用s来替代结点p，然后在删除此结点s：

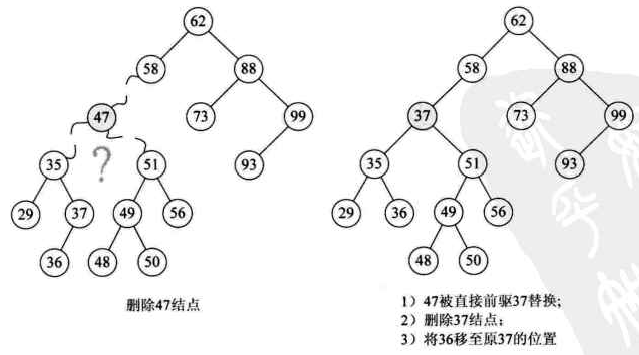
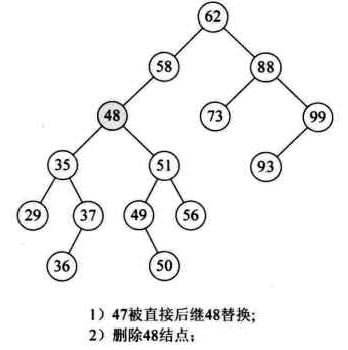
二叉排序树总结

二叉排序树是以链接的方式存储，保持了链接存储结构在执行插入或删除操作是不用移动元素的优点，只要找到合适的插入和删除位置后，仅需要修改链接指针即可，因此插入删除的时间性能比较好。

对于二叉排序树查找，走的就是从根结点到要查找的结点的路径，其比较次数等于给定值的结点在二叉排序树的层数。极端情况，最少为一次，即根结点就是要找的结点，最多也不会超过树的深度。也就是说，二叉排序树的查找性能取决于二叉排序树的形状。可问题在于二叉排序树的形状是不确定的。

例如{62,88,58,47,35,73,51,99,37,93}这样的数组，我们可以构建如下左图的二叉排序树。如果数组元素的次序是从小到大有序，如{35,37,47,51,58,62,73,88,93,99}，则二叉排序树就成了极端的右斜树，但它依然是一颗二叉排序树。同样是查找点99，左图只需要两次比较，而右图就需要10次比较才可以得到结果，二者差异很大。

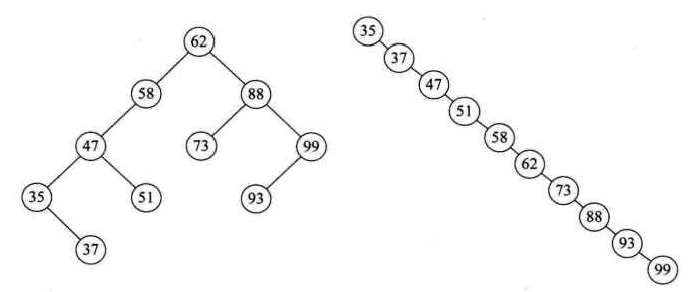
也就是说，我们希望二叉排序树是比较平衡的，即其深度与完全二叉树相同，均为[log2n]+1，那么查找的时间复杂度为O(logn)，近似于折半查找。不平衡的最坏情况就是上图的右斜树，查找时间复杂度为O(n)，这等同于顺序查找。

我们希望对一个集合按二叉排序树查找，最好是把它构建成一颗平衡二叉排序树。