全组合算法
从n中选m个数
(1) 递归
a. 首先从n个数中选取编号最大的数,然后在剩下的n-1个数里面选取m-1个数,直到从n-(m-1)个数中选取1个数为止。
b. 从n个数中选取编号次小的一个数,继续执行1步,直到当前可选编号最大的数为m。
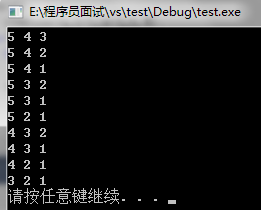
例如在:1 2 3 4 5选取3个数,n=5,m=3:
1 2 3
1 2 4
1 2 5
1 3 4
1 3 5
1 4 5
2 3 4
2 3 5
2 4 5
3 4 5
从中可以找到规律 最高位可以取5~3:n~m
次高位可以取4~2:n-1~m-1
最低为可以取3~1:n-2~m-2
代码实现:
#include <iostream>
using namespace std;
void combine(int a[],int n,int m,int b[],const int M){
for(int i=n;i>=m;i--){ //注意这里的循环范围 负责当前这一位的数据构造
b[m-1]=i-1; //从最大编号开始
if(m>1)
combine(a,i-1,m-1,b,M); //构造下一位的数据 n-1和m-1
else{ //m == 1 输出一个组合
for(int j=M-1;j>=0;j--)
cout<<a[b[j]]<<" ";
cout<<endl;
}
}
}
int main(){
int n=5;
int a[5];
for(int i=0;i<n;i++)
a[i]=i+1;
const int M=3;
int m=M;
int b[M];
combine(a,n,m,b,M);
system("pause");
}
(2)01转换法
本程序的思路是开一个数组,其下标表示1到n个数,数组元素的值为1表示其代表的数被选中,为0则没选中。首先初始化,将数组前n个元素置1,表示第一个组合为前n个数。
然后从左到右扫描数组元素值的“10”组合,找到第一个“10”组合后将其变为“01”组合,同时将其左边的所有“1”全部移动到数组的最左端。
当第一个“1”移动到数组的n-m的位置,即n个“1”全部移动到最右端时,就得到了最后一个组合。
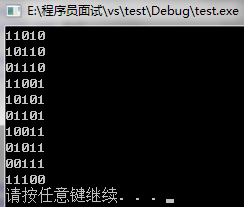
例如求5中选3的组合:
1 1 1 0 0 //1,2,3
1 1 0 1 0 //1,2,4
1 0 1 1 0 //1,3,4
0 1 1 1 0 //2,3,4
1 1 0 0 1 //1,2,5
1 0 1 0 1 //1,3,5
0 1 1 0 1 //2,3,5
1 0 0 1 1 //1,4,5
0 1 0 1 1 //2,4,5
0 0 1 1 1 //3,4,5
代码实现:
#include <iostream>
using namespace std;
void main(){
const int M=5;
const int N=8;
int arr[N];
for(int i=0;i<N;i++){ //把前M位都置为1 其他置为0
if(i<M)
arr[i]=1;
else
arr[i]=0;
}
bool loop=true;
while(loop){
bool ifzero=false; //标记前面是否有0
int i;
loop=false; //把loop置为false
for(i=0;i<N;i++){
if(arr[i]==0)
ifzero=true;
if(arr[i]==1&&arr[i+1]==0){ //查找第一个等于10的位置
arr[i]=0;
arr[i+1]=1; //把10地方变为01
loop=true; //如果没有10变为01 表明已经结束完成
break;
}
}
if(ifzero==true){ //如果10前面有0 则从下标0到i-1开始反转
for(int j=0;j<i/2;j++){
int temp=arr[j];
arr[j]=arr[i-1-j];
arr[i-1-j]=temp;
}
}
for(int j=0;j<N;j++)
cout<<arr[j];
cout<<endl;
}
system("pause");
}
列出所有子集–二进制法
编写一个程序,列出{1,2,3,…,n}这个集合的所有子集,包括空集合。
可以使用二进制的第i位表示是否包含集合的第i个元素,如数字6的二进制形式是110,表示取集合的第2,3两个元素组成的子集。
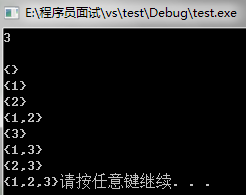
比如{1,2,3}的子集为
0 0 1—–1——-对应整数1
0 1 0—–2——-对应整数2
0 1 1—–1 2—–对应整数3
1 0 0—–3——-对应整数4
1 0 1—–1 3—–对应整数5
1 1 0—–2 3—–对应整数6
1 1 1—–1 2 3—对应整数7
可以看出子集的规律是按照递进方式进行的。
由000变成001,由001变成010,由010变成011….。算法是首先寻找第一个0的位置,并且把该位置置1,同时该位置前面的1都置为0,就得到一个组合。
#include <iostream>
using namespace std;
#define MAXSIZE 20
#define LOOP 1
void main(){
char digit[MAXSIZE];
int i,j;
int n;
cin>>n;
for(i = 0; i < n; i++) //初始化全为0
digit[i] = '0';
printf("\n( )"); //输出空集合
while(LOOP){
for(i = 0;i < n && digit[i] == '1';i++) //找到第一个0的位置
digit[i]='0';
if (i == n) //如果全为1 表示集合输出完成
break;
else
digit[i]='1'; //把第一个0的位置 把它置为1
for (i = 0; i < n && digit[i] == '0'; i++); //找到第一个1的位置 开始打印结果
printf("\n(%d",i+1);
for (j=i + 1;j<n;j++) //有多少个1就打印多少个
if(digit[j] == '1')
printf(",%d", j + 1);
printf(")");
}
system("pause");
}
列出所有子集——字典顺序
编写一个程序,用字典顺序(Lexical Order)把一个集合的所有子集找出来。
说明:如果不知道何谓字典顺序,在此作一个简单的说明。假设给定的集合有n个元素,
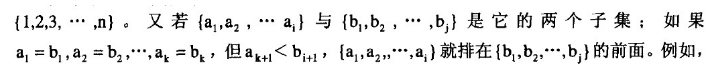
{1,2,3,4}与{1,2,4}是两集合,它们前面的两个元素相同,但第三个不同,因此包含小的元 素的集合就排在前面。请回想一下,这与字符串的比较有什么不一样呢?完全相同,惟一的差异,就是在集合中的元素要从小到大排好。
下面左边是n=3,右边是n=4的结果,如表3-1所示:
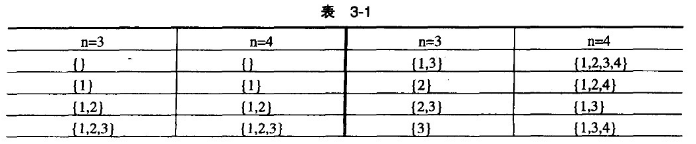
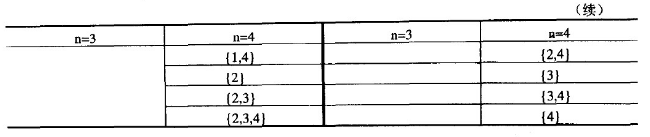
事实上,这是一个十分简单的程序,除了空集合之外,最“小”的一个集合就是{1}再下一个就是包含1,而且再加上1的下一个元素(1+1=2)的集合,即{1,2};
下一个元素 自然就是含有1与2,并且还有2的下一个元素(2+1=3)的集合{1,2,3}了。就这样一直到包含了所有元素为止,亦即{1,2,3,····,n}。下一个集合是谁?绝不是{1,2,3,…,n-1},因为它比{1,2,3,…,n}小,事实上应该是{1,2,3,…,n-2,n}。为什么呢?在{1,2,3,…,n-1,n}与 {1,2,3,…,n-2,n}之间,前n-2个元素完全相同,但是n-1<n,这不就证实了以上说法了吗?
由于以上原因,因此可以用一个数组set[]来存放集合的元素,一开始时set[0]=1,表 示{1};
另外,用一个变量position,指出目前最右边的位置何在,在开始时自然就是1。接下来,就陆续地产生下一个集合了。注意,目前集合中最右边的元素是set[position],如 果它的值比n小,那就表示还可以加进一个元素,就像是从{1,2,3}加上一个元素变成{1,2,3, 4}一样(n>4)。这倒是容易做,下一个元素在set[position+1],因此在那存入set[position+1] 这个值就行了;
同时position也向右移一位。如果目前最右边元素set [position]已经是n,因而不能再增加元素了。例如,当n=4时,如果有{1,3,4},那自然不能像前面所说的加入一个5。这时看最右边元素的位置,亦即position,是不是在第一位(如果n=6,而现在的集合是{6}),如果不在第一位,那就可以往回移一位,并且把那个位置的值加上1。例如,如果现在有{1,3,4},而n=4;最右边(4)的位置不是在第一位,因而退回一位,等于是{1,3};但这是不对的,因为{1,3}比{1,3,4} “小”,要做得比{1,3,4}大,把3加上1而变成{1,4}就行了。如果最右边(4)的位置是在第一位,那么程序就完成了。
#include <iostream>
using namespace std;
void main(){
const int M=4;
int arr[M];
int pos=0;
arr[0]=1;
cout<<arr[0]<<endl;
bool loop=true;
while(loop){
if(arr[pos]!=M){
pos++;
arr[pos]=arr[pos-1]+1;
}else{
if(pos==0&&arr[pos]==M) //当pos指向第一个该位置并且该位置的值是M 结束循环
break;
else{
pos--;
arr[pos]=arr[pos]+1; //对应的位置增1
}
}
for(int i=0;i<=pos;i++) //打印子集
cout<<arr[i]<<" ";
cout<<endl;
}
system("pause");
}
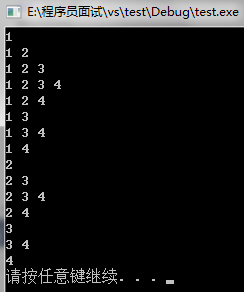
列出所有子集——递归方法
#include <iostream>
#include <vector>
#include <string>
using namespace std;
void dfc(vector<int> &vec,int pos,string str){
for(int i=pos;i<vec.size();i++){
str.push_back(vec[i]+'0');
cout<<str<<endl;
dfc(vec,i+1,str);
str.pop_back();
//while(i<vec.size()-1&&vec[i]==vec[i+1])
// i++;
}
}
int main(){
vector<int> vec;
vec.push_back(1);
vec.push_back(2);
//vec.push_back(2);
vec.push_back(3);
string str;
dfc(vec,0,str);
system("pause");
}
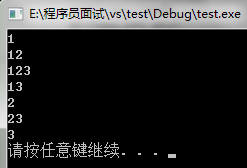
全排序算法
stl_函数实现全排序
在#include
next_permutation(a,a+len);
返回的是一个bool类型的值;直到找不到全排列为止,返回false。并且对全排列重复出现的情况可以过滤,即最后得出的全排列的结果中,不会有相同的出现。并且貌似只能从小到大的产生排列,也就是说,如果a中的字符串为刚好从大到小,那么就一组都产生不了。
#include<iostream>
#include<algorithm>
using namespace std;
int main(){
const int len=3;
int a[len]={1,2,3};
sort(a,a+len);
for(int i=0;i<len;i++)
cout<<a[i]<<" ";
cout<<endl;
while(next_permutation(a,a+3)){
for(int i=0;i<len;i++)
cout<<a[i]<<" ";
cout<<endl;
}
system("pause");
}
#include<iostream>
#include<algorithm>
using namespace std;
char a[100];
int main(){
cin>>a;
int len=strlen(a);
sort(a,a+len);
cout<<a<<endl;
while(next_permutation(a,a+len)){
cout<<a<<endl;
}
system("pause");
}
递归实现全排列
为方便起见,用123来示例下。123的全排列有123、132、213、231、312、321这六种。首先考虑213和321这二个数是如何得出的。显然这二个都是123中的1与后面两数交换得到的。然后可以将123的第二个数和每三个数交换得到132。同理可以根据213和321来得231和312。因此可以知道——全排列就是从第一个数字起每个数分别与它后面的数字交换。
1 2 3:(0 1位置交换 pos=0)2 1 3:(1 2位置交换 pos=1)2 3 1
1 2 3:(0 2位置交换 pos=0)3 2 1:(1 2位置交换 pos=1)3 1 2
1 2 3:(1 2位置交换 pos=1)1 3 2
#include <iostream>
using namespace std;
void swap(int a[],int i,int j){ //交换数组a中i和j位置的元素
int temp=a[i];
a[i]=a[j];
a[j]=temp;
}
void permutaion(int a[],int k,int m){ //m表示数组元素的个数
for(int j=k;j<m-1;j++){
for(int i=j+1;i<m;i++){
swap(a,j,i); //交换
for(int i=0;i<m;i++) //打印序列
cout<<a[i]<<" ";
cout<<endl;
permutaion(a,j+1,m); //开始递归下一个位置
swap(a,j,i); //又将其交换回来
}
}
}
int main(){
const int len=3;
int a[len]={1,2,3};
for(int i=0;i<len;i++) //打印序列
cout<<a[i]<<" ";
cout<<endl;
permutaion(a,0,len);
system("pause");
}
插入法实现全排序
例如1 2 3,先把1取出来:
1
然乎把2取出来,插入1的左右两边得:
2 1
1 2
把3取出来,分别插入到以上两组数据中:
3 2 1
2 3 1
2 1 3
3 1 2
1 3 2
1 2 3
代码实现:
#include <iostream>
#include <list>
#include <string>
using namespace std;
int main(){
char a[10]; //输入字符串
cin>>a;
int len=strlen(a);
string s1; //获取第一个字符
s1=s1+a[0];
list<string> L;
L.push_back(s1);
cout<<endl;
for(int i=1;i<len;i++){ //从第二个字符开始 把它插入L中的每一个字符中
int listsize=L.size(); //求出list的长度
for(int j=0;j<listsize;j++){
string strfront=L.front(); //L出队列
L.pop_front();
int lensf=strfront.length(); //求出字符串长度 确定插入次数
for(int k=0;k<=lensf;k++){
char c=a[i];
string tp=strfront;
tp.insert(k,1,c);
L.push_back(tp);
}
}
}
list<string>::iterator it;
for(it=L.begin();it!=L.end();it++)
cout<<*it<<endl;
system("pause");
}
去掉重复的全排列的递归实现
由于全排列就是从第一个数字起每个数分别与它后面的数字交换。我们先尝试加个这样的判断——如果一个数与后面的数字相同那么这二个数就不交换了。如122,第一个数与后面交换得212、221。然后122中第二数就不用与第三个数交换了,但对212,它第二个数与第三个数是不相同的,交换之后得到221。与由122中第一个数与第三个数交换所得的221重复了。所以这个方法不行。
换种思维,对122,第一个数1与第二个数2交换得到212,然后考虑第一个数1与第三个数2交换,此时由于第三个数等于第二个数,所以第一个数不再与第三个数交换。再考虑212,它的第二个数与第三个数交换可以得到解决221。此时全排列生成完毕。
这样我们也得到了在全排列中去掉重复的规则——去重的全排列就是从第一个数字起每个数分别与它后面非重复出现的数字交换。用编程的话描述就是第i个数与第j个数交换时,要求[i,j)中没有与第j个数相等的数。下面给出完整代码:
#include <iostream>
using namespace std;
void swap(int a[],int i,int j){ //交换数组a中i和j位置的元素
int temp=a[i];
a[i]=a[j];
a[j]=temp;
}
bool repeat(int a[],int j,int i){
for(int x=j;x<i;x++){
if(a[x]==a[i]){
return true;
}
}
return false;
}
void permutaion(int a[],int k,int m){ //m表示数组元素的个数
for(int j=k;j<m-1;j++){
for(int i=j+1;i<m;i++){
if(!repeat(a,j,i)){ //判断要交换的数据是否跟前面的数据重复
swap(a,j,i); //交换
for(int i=0;i<m;i++) //打印序列
cout<<a[i]<<" ";
cout<<endl;
permutaion(a,j+1,m); //开始递归下一个位置
swap(a,j,i); //又将其交换回来
}
}
}
}
int main(){
const int len=3;
int a[len]={1,2,2};
for(int i=0;i<len;i++) //打印序列
cout<<a[i]<<" ";
cout<<endl;
permutaion(a,0,len);
system("pause");
}
全排列的非递归实现
要考虑全排列的非递归实现,先来考虑如何计算字符串的下一个排列。如“1234”的下一个排列就是“1243”。只要对字符串反复求出下一个排列,全排列的也就迎刃而解了。
如何计算字符串的下一个排列了?来考虑“926520”这个字符串,我们从后向前找第一双相邻的递增数字,“20”、“52”都是非递增的,“26”即满足要求,称前一个数字2为替换数,替换数的下标称为替换点,再从后面找一个比替换数大的最小数(这个数必然存在),0、2都不行,5可以,将5和2交换得到“956220”,然后再将替换点后的字符串“6220”颠倒即得到“950226”。
对于像“4321”这种已经是最“大”的排列,采用STL中的处理方法,将字符串整个颠倒得到最“小”的排列”1234”并返回false。
动态规划算法
什么是动态规划(简称DP)
动态规划算法通常基于一个递推公式及一个或多个初始状态。 当前子问题的解将由上一次子问题的解推出。使用动态规划来解题只需要多项式时间复杂度, 因此它比回溯法、暴力法等要快许多。首先,我们要找到某个状态的最优解,然后在它的帮助下,找到下一个状态的最优解。
动态规划入门例子–凑钱
如果我们有面值为1元、3元和5元的硬币若干枚,如何用最少的硬币凑够11元?
如何用最少的硬币凑够i元(i<11)?当i=0,即我们需要多少个硬币来凑够0元。 由于1,3,5都大于0,即没有比0小的币值,因此凑够0元我们最少需要0个硬币。我们用d(i)=j来表示凑够i元最少需要j个硬币。于是我们已经得到了d(0)=0, 表示凑够0元最小需要0个硬币。
当i=1时,只有面值为1元的硬币可用,因此我们拿起一个面值为1的硬币,接下来只需要凑够0元即可,而这个是已经知道答案的,即d(0)=0。所以,d(1)=d(1-1)+1=d(0)+1=0+1=1。
当i=2时,仍然只有面值为1的硬币可用,于是我拿起一个面值为1的硬币,接下来我只需要再凑够2-1=1元即可(记得要用最小的硬币数量)。所以d(2)=d(2-1)+1=d(1)+1=1+1=2。
当i=3时,我们能用的硬币就有两种了:1元的和3元的( 5元的仍然没用,因为你需要凑的数目是3元!)。 既然能用的硬币有两种,我就有两种方案。如果我拿了一个1元的硬币,我的目标就变为了:凑够3-1=2元需要的最少硬币数量。即d(3)=d(3-1)+1=d(2)+1=2+1=3。这个方案说的是,我拿3个1元的硬币;第二种方案是我拿起一个3元的硬币,我的目标就变成:凑够3-3=0元需要的最少硬币数量。即d(3)=d(3-3)+1=d(0)+1=0+1=1。这个方案说的是,我拿1个3元的硬币。要用最少的硬币数量来凑够3元的,所以选择d(3)=1。具体是这样得到的:d(3)=min{d(3-1)+1, d(3-3)+1}。
具体分析过程如下:
d(0)=0;
d(1)=d(1-1)+1=1; //可用1元
d(2)=d(2-1)+1=d(1)+1=2;
d(3)=min{d(3-1)+1,d(3-3)+1}=1; //可用1、3元
d(4)=min{d(4-1)+1,d(4-3)+1}=2; //可用1、3元
d(5)=min{d(5-1)+1,d(5-3)+1,d(5-5)+1}=1; //可用1、3、5元
实现代码:
#include <iostream>
using namespace std;
int main(){
int n;
const int m=3;
int arr[m]={1,3,5}; //钱的币值
while(cin>>n){
int *d=(int*)malloc((n+1)*sizeof(int));
d[0]=0;
for(int i=1;i<=n;i++){ //每一次状态的下标
int min;
for(int j=0;j<m&&i>=arr[j];j++){
if(j==0){
min=d[i-arr[j]]+1;
}else{
if(min>d[i-arr[j]]+1)
min=d[i-arr[j]]+1;
}
}
d[i]=min;
}
cout<<d[n]<<endl;
}
}
动态规划入门例子–最长非降子序列
一个序列有N个数:A[1],A[2],…,A[N],求出最长非降子序列的长度。 (DP问题LIS:longest increasing subsequence)
例如有序列:
5,3,4,8,6,7
前1个数的LIS长度d(1)=1(序列:5)
前2个数的LIS长度d(2)=1(序列:3; 3前面没有比3小的)
前3个数的LIS长度d(3)=2(序列:3,4; 4前面有个比它小的3,所以d(3)=d(2)+1)
前4个数的LIS长度d(4)=3(序列:3,4,8; 8前面比它小的有3个数,所以d(4)=max{d(1),d(2),d(3)}+1=3)
如果我们已经求出了d(1)到d(i-1),那么d(i)可以用下面的状态转移方程得到:
d(i)=max{1, d(j)+1} ,其中j<i,A[j]<=A[i]
想要求d(i),就把i前面的各个子序列中,最后一个数不大于A[i]的序列长度加1,然后取出最大的长度即为d(i)。 当然有可能i前面的各个子序列中最后一个数都大于A[i],那么d(i)=1,即它自身成为一个长度为1的子序列。
代码实现:
#include <iostream>
using namespace std;
int main(){
const int n=6;
int arr[n]={5,3,4,8,6,7};
int d[n];
for(int i=0;i<n;i++){
d[i]=1;
for(int j=0;j<i;j++){
if(d[j]>=d[i]){
if(arr[i]>=arr[j]) //判断是否加进来
d[i]=d[j]+1;
else
d[i]=d[j];
}
}
}
cout<<d[n-1]<<endl; //输出4
system("pause");
}
该算法的时间复杂度是O(n^2)。
动态规划入门例子–最短路线问题
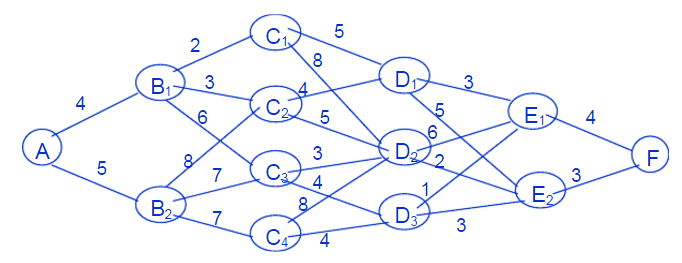
可以画出如下图:
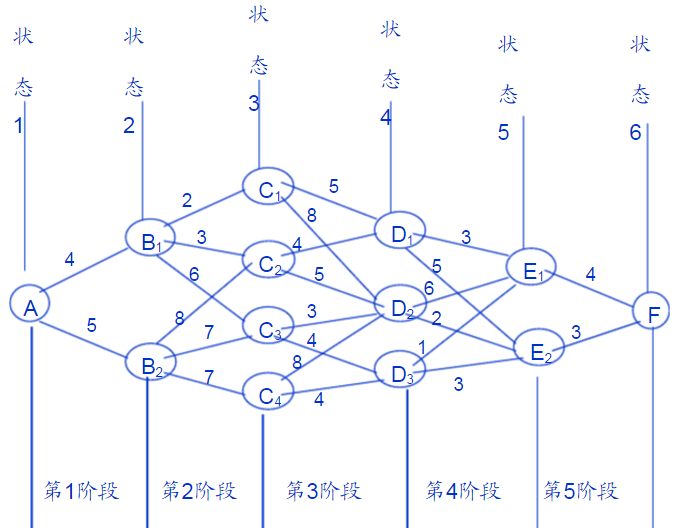

动态规划入门例子–解决二维的DP问题
平面上有N*M个格子,每个格子中放着一定数量的苹果。你从左上角的格子开始,每一步只能向下走或是向右走,每次走到一个格子上就把格子里的苹果收集起来,这样下去,你最多能收集到多少个苹果。
解这个问题与解其它的DP问题几乎没有什么两样。第一步找到问题的“状态”, 第二步找到“状态转移方程”,然后基本上问题就解决了。
到达一个格子的方式最多只有两种:从左边来的(除了第一列)和从上边来的(除了第一行)。因此为了求出到达当前格子后最多能收集到多少个苹果,我们就要先去考察那些能到达当前这个格子的格子,到达它们最多能收集到多少个苹果。
状态S[i][j]表示我们走到(i,j)这个格子时,最多能收集到多少个苹果。状态转移方程如下:
S[i][j]=A[i][j] + max(S[i-1][j], if i>0 ; S[i][j-1], if j>0)
其中i代表行,j代表列,下标均从0开始;A[i][j]代表格子(i,j)处的苹果数量。
S[i][j]有两种计算方式:
1.对于每一行,从左向右计算,然后从上到下逐行处理;
2.对于每一列,从上到下计算,然后从左向右逐列处理。
这样做的目的是为了在计算S[i][j]时,S[i-1][j]和S[i][j-1]都已经计算出来了。
```cpp for(int i=0;i<N;i++){ for(int j=0;j<N;j++){ s[i][j]=A[i][j]+max(s[i][j-1],if j>0;s[i-1][j],if i>0); } }