最优树的定义
结点的路径长度定义为:
从根结点到该结点的路径上分支的数目。
树的路径长度定义为:
树中每个结点的路径长度之和。
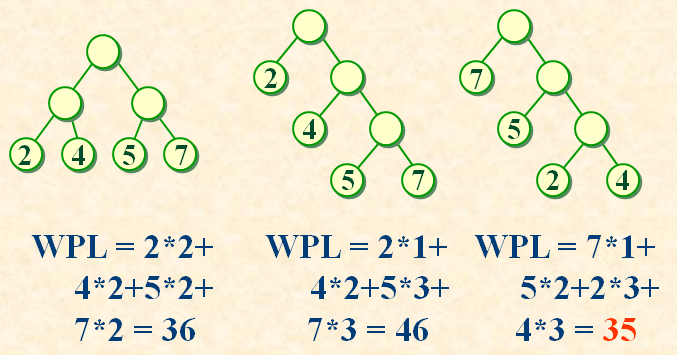
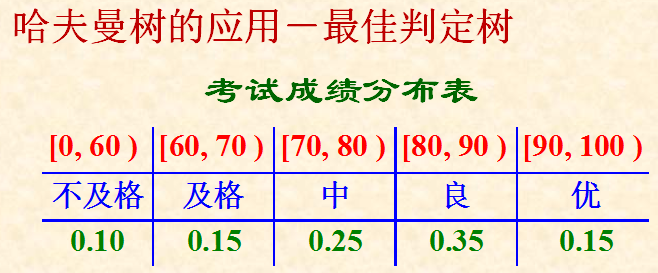
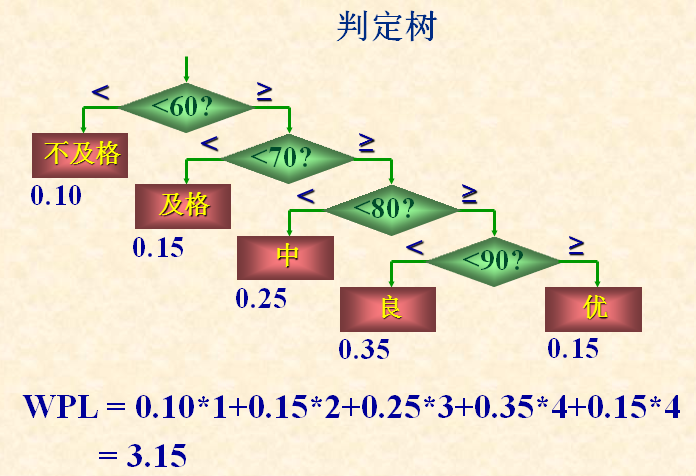
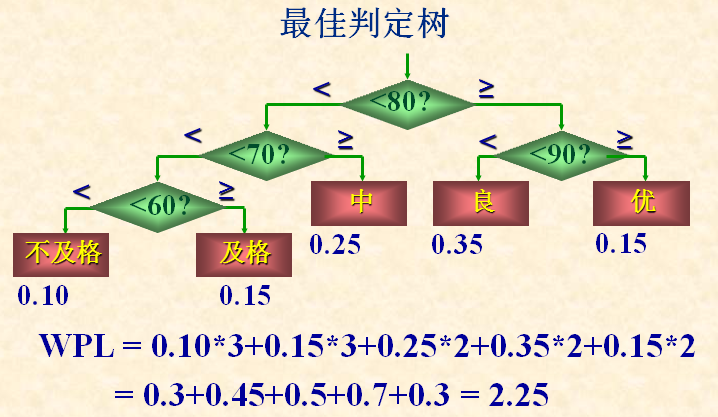
树的带权路径长度定义为:
树中所有叶子结点的带权路径长度之和。

假设有n权值{w1,w2…wn},试构造一颗有n个叶子结点的二叉树,每个叶子结点带权为wi,则其中带权路径长度取最小值的树,称为“最优树二叉树”或“哈夫曼树”。
如何构造最优树
(哈夫曼算法)以二叉树为例:
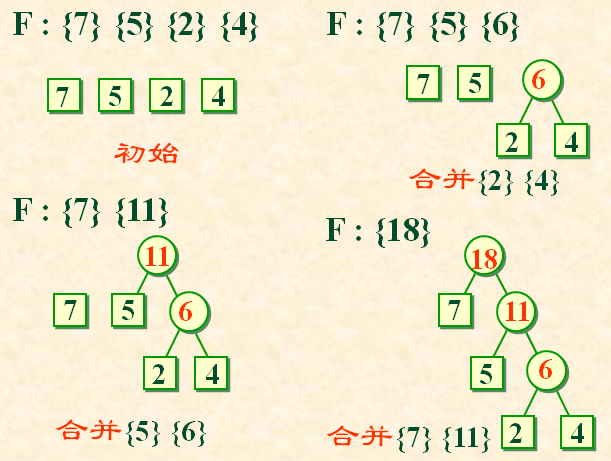
(1)根据给定的n个权值{w1, w2, …, wn},构造n棵二叉树的集合:
F = {T1,T2,…, Tn},
其中每棵二叉树中均只含一个带权值为wi的根结点,其左、右子树为空树;
(2)在F中选取其根结点的权值为最小的两棵二叉树,分别作为左、右子树构造一棵新的二叉树,并置这棵新的二叉树根结点的权值为其左、右子树根结点的权值之和;
(3)从F中删去这两棵树,同时加入刚生成的新树;
(4)重复 (2) 和 (3) 两步,直至F中只含一棵树为止。
哈夫曼树中没有度为1的结点(这类树又称严格的或正则的)二叉树。
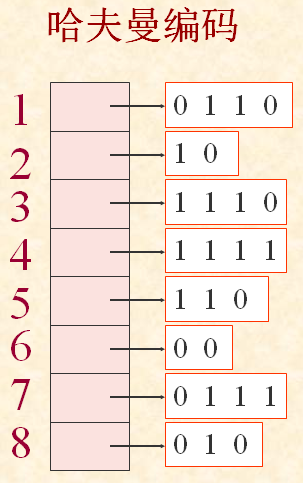
哈夫曼编码
指的是,任何一个字符的编码都不是同一字符集中另一个字符的编码的前缀。
利用哈夫曼树可以构造一种不等长的二进制编码,并且构造所得的哈夫曼编码是一种最优前缀编码,即使所传电文的总长度最短。
非等长字符编码时,一个字符的编码不能是另一个字符编码的前缀:

哈夫曼编码主要用途是实现数据压缩。设给出一段报文:
CAST CAST SAT AT A TASA
字符集合是 { A, C, S, T },各个字符出现的频度(次数)是 W={ 7, 2, 4, 5 }。
若给每个字符以等长编码:
A : 00 C : 01 S : 10 T : 11
则总编码长度为 ( 2+7+4+5 ) * 2 = 36。
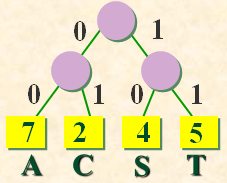
若按各个字符出现的概率不同而给予不等长编码,可望减少总编码长度。
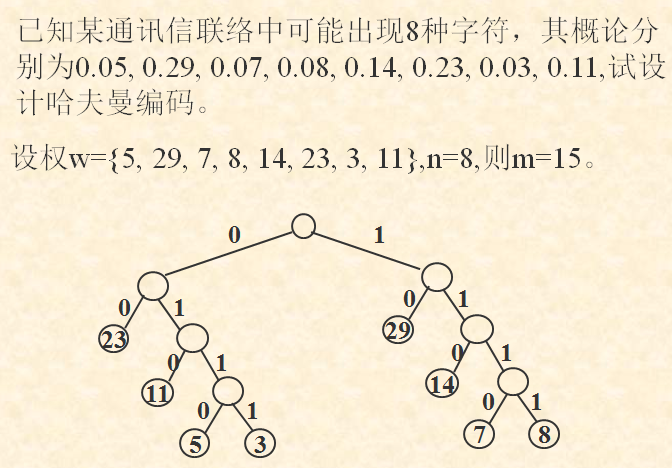
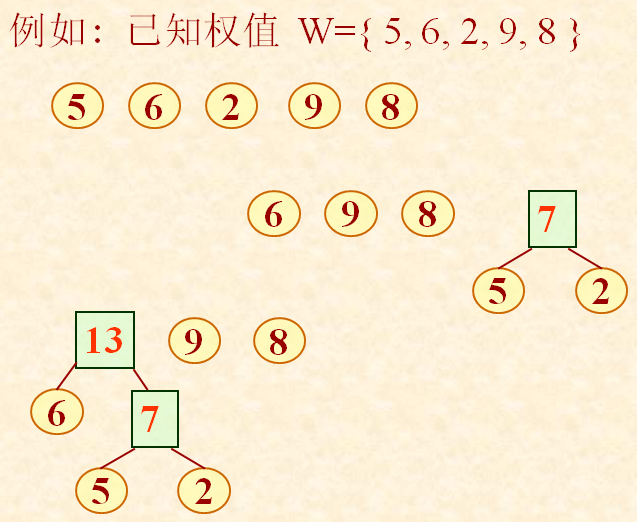
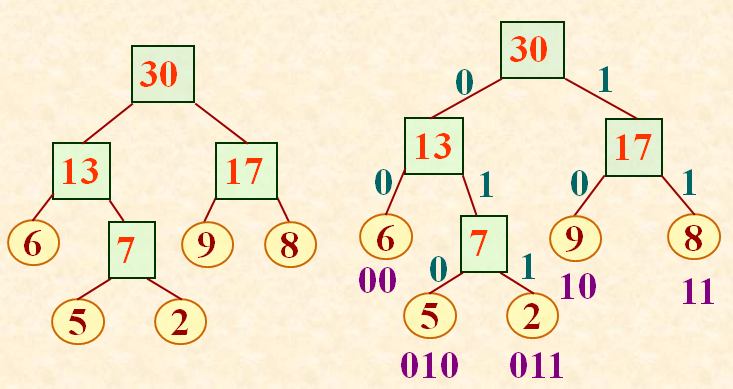
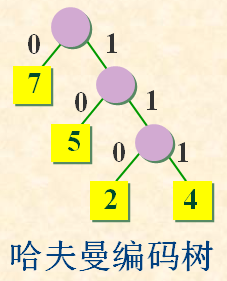
各字符出现概率为{ 2/18, 7/18, 4/18, 5/18 },化整为 { 2, 7, 4, 5 }。以它们为各叶结点上的权值,建立哈夫曼树。左分支赋0,右分支赋1,得哈夫曼编码(变长编码):
A : 0 T : 10 C : 110 S : 111
它的总编码长度:7*1+5*2+( 2+4 )*3 = 35。比等长编码的情形要短。总编码长度正好等于哈夫曼树的带权路径长度WPL。哈夫曼编码是一种前缀编码。解码时不会混淆。
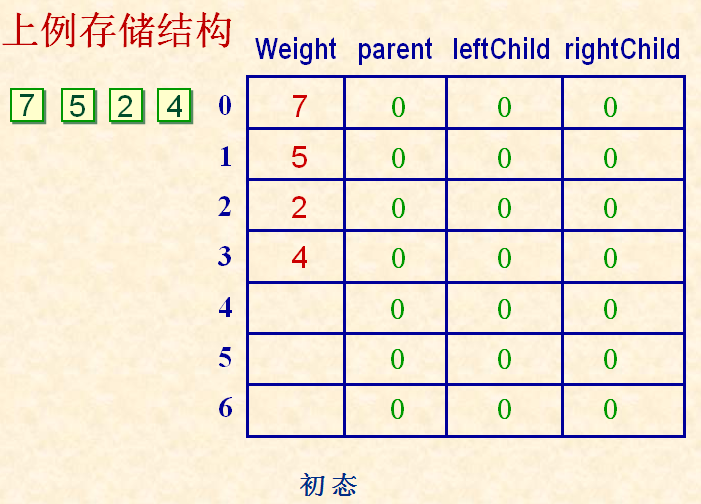
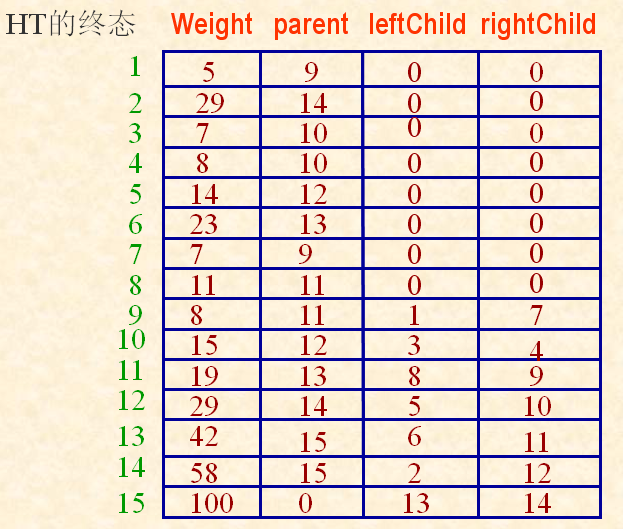
哈夫曼树的存储表示
typedef struct {
unsigned int weight;
unsigned int parent, lchild, rchild;
} HTNode,*HuffmanTree;

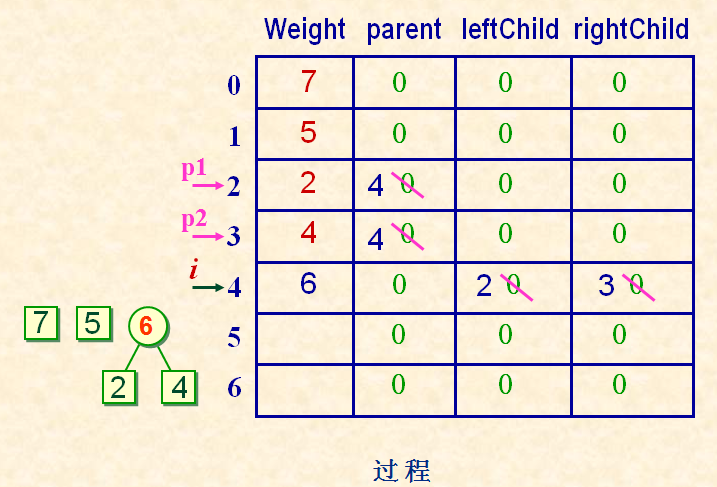
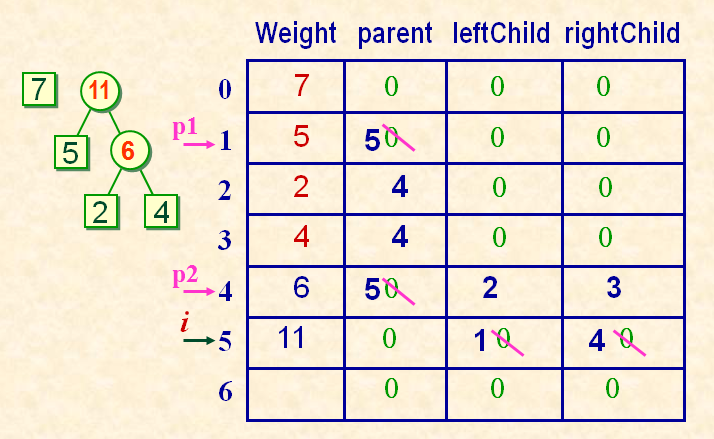
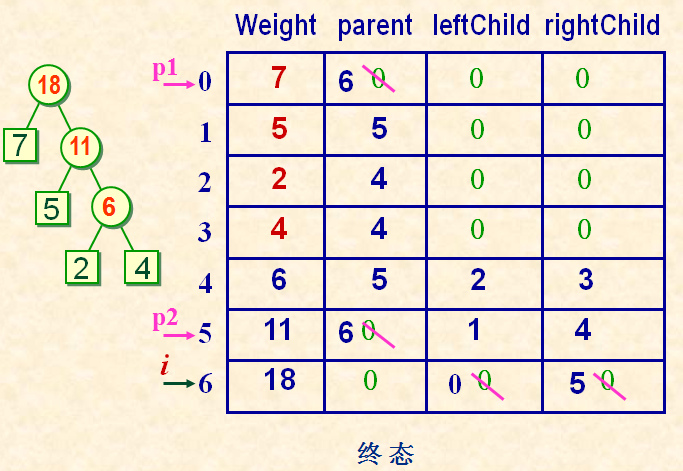
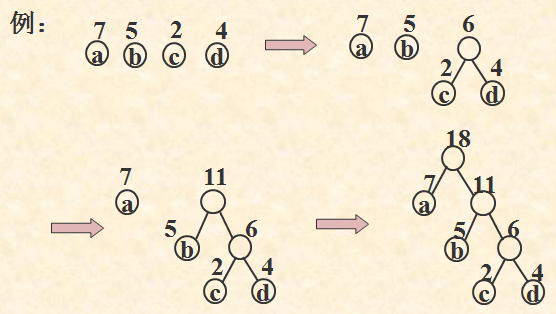
举例哈夫曼树的构造过程: