树的存储结构
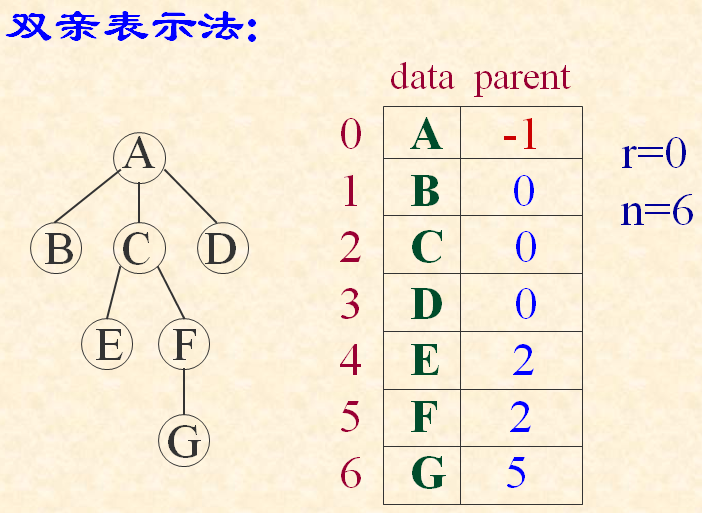
1.双亲表示法

#define MAX_TREE_SIZE 100
typedef struct PTNode {
Elem data;
int parent; //双亲位置域
}PTNode;
树的结构:
typedef struct {
PTNode nodes[MAX_TREE_SIZE];
int r,n; // 根结点的位置和结点个数
} PTree;
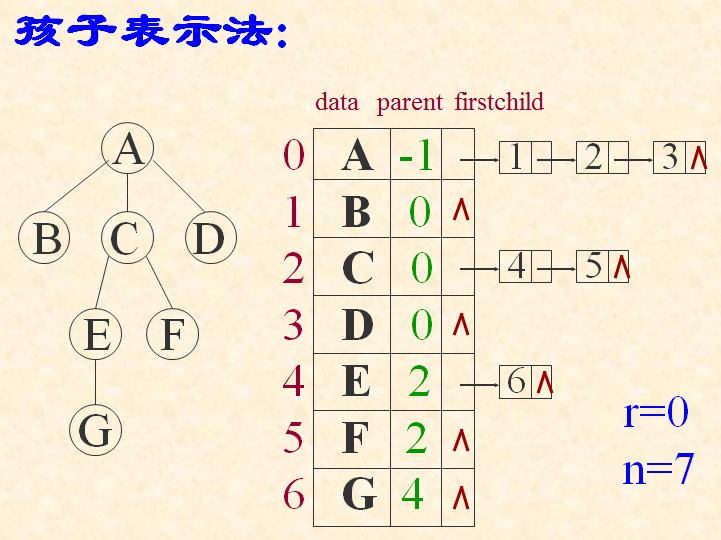
2.孩子表示法:

typedef struct CTNode {
int child;
struct CTNode *nextchild;
}*ChildPtr;

typedef struct {
Elem data;
ChildPtr firstchild; //孩子链的头指针
}CTBox;
树的结构:
typedef struct {
CTBox nodes[MAX_TREE_SIZE];
int n,r; //结点数和根结点的位置
}CTree;
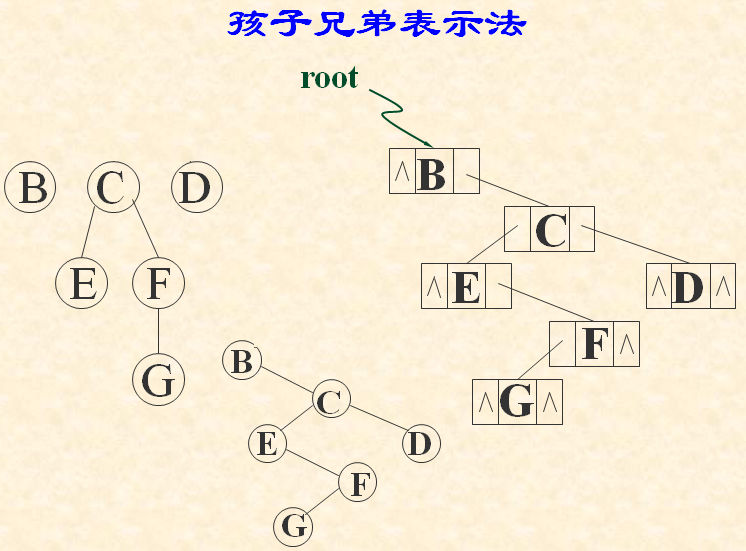
3.孩子兄弟表示法

typedef struct CSNode{
Elem data;
struct CSNode *firstchild,*nextsibling;
}CSNode,*CSTree;
树和二叉树的转换
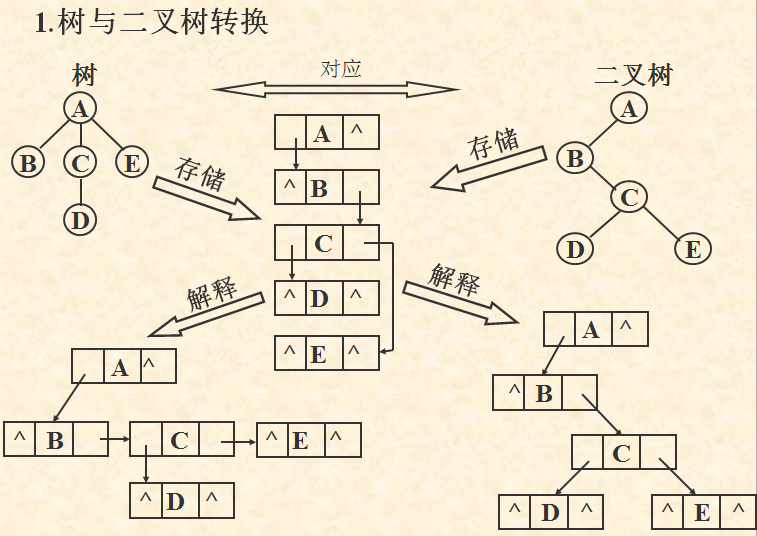
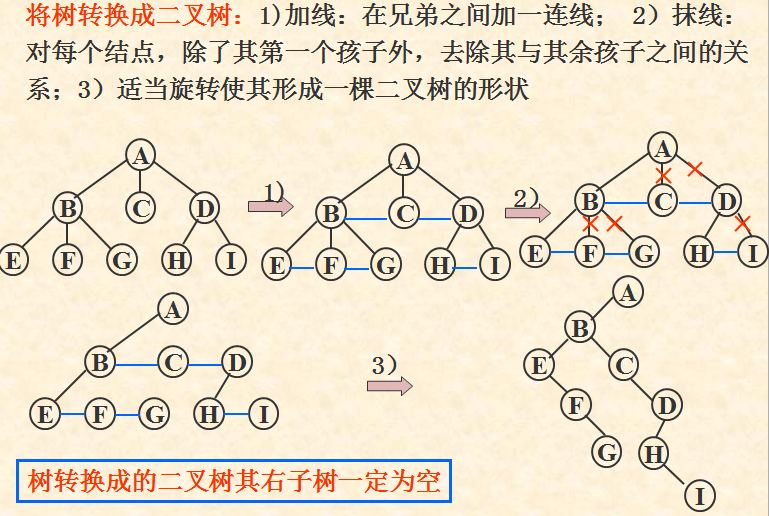
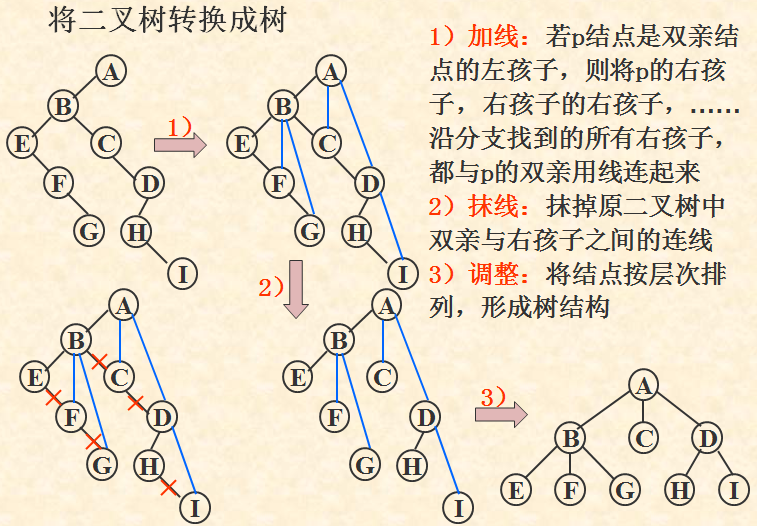
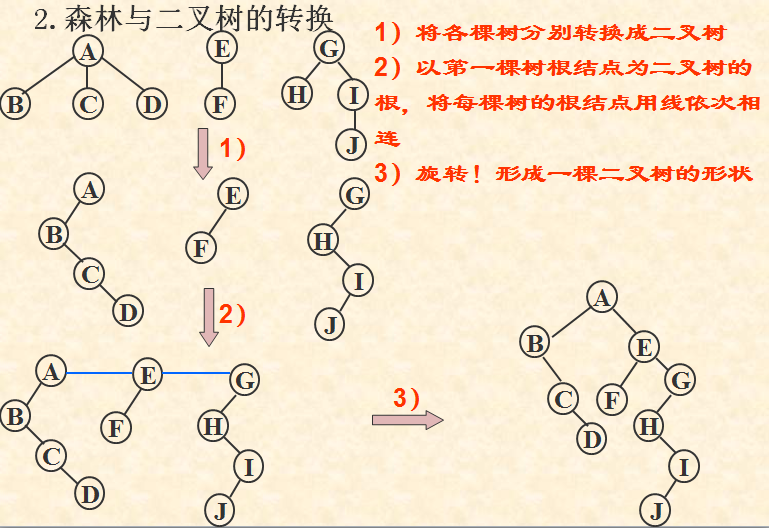
由此,树和森林的各种操作均可与二叉树的各种操作相对应。应当注意的是,和树对应的二叉树,其左、右子树的概念已改变为:左是孩子,右是兄弟
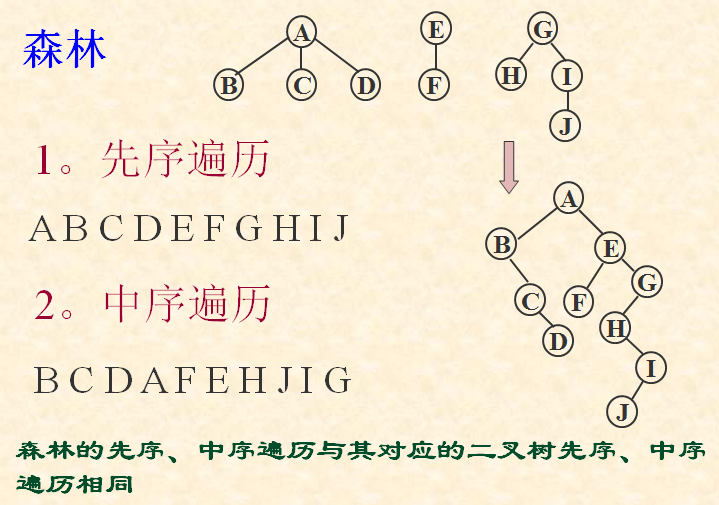
树和森林的遍历
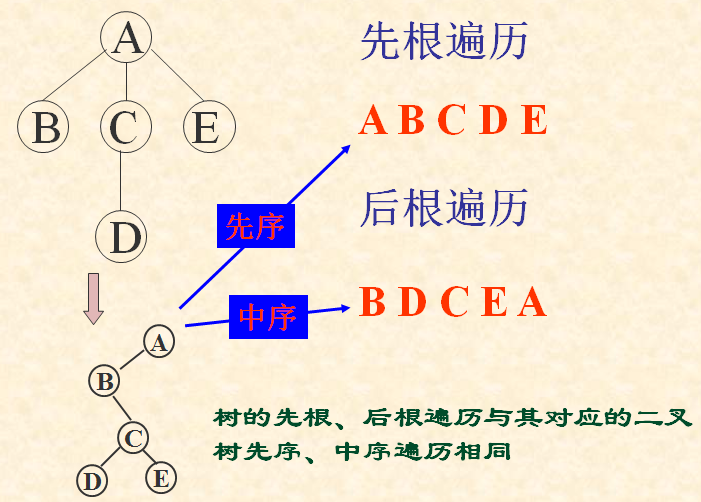
1.先根(次序)遍历:
若树不空,则先访问根结点,然后依次先根遍历各棵子树。
2.后根(次序)遍历:
若树不空,则先依次后根遍历各棵子树,然后访问根结点。
先序遍历森林:
若森林不空,则:
访问森林中第一棵树的根结点;
先序遍历森林中第一棵树中根结点的子树森林;
先序遍历森林中(除第一棵树之外)其余树构成的森林。
即:依次从左至右对森林中的每一棵树进行先根遍历。