归并排序算法
归并排序(Merging Sort)就是利用归并的思想实现的排序方法。它的原理是假设初始序列含有n个记录,则可以看出是n个有序的子序列,每个子序列的长度为1,然后两两归并,得到[n/2]([x]表示不小于x的最小整数)个长度为2或1的有序子序列;再两两归并,….如此重复,直至得到一个程度为n的有序序列为止,这种排序方法称为2路归并排序。
例如我们要对序列{50,10,90,30,70,40,80,60,20}进行排序,排序过程为:
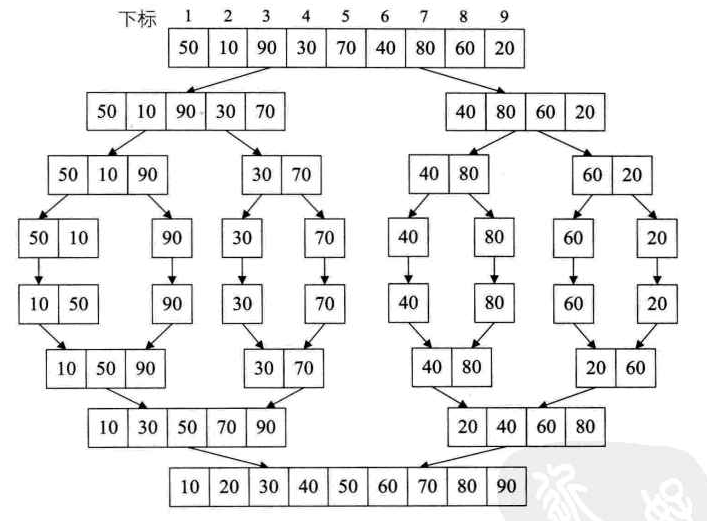
程序代码实现
#include <iostream>
using namespace std;
#define MAXSIZE 10 //用于排序数组个数最大值 可根据需要修改
typedef struct{
int r[MAXSIZE]; //数组
int lengh; //数组的实际长度
}SqList;
void print(SqList *L){ //打印数组
for(int i=0;i<L->lengh;i++){
cout<<L->r[i]<<" ";
}
cout<<endl;
}
//i为数组开始标号 m为数组分隔标号 n为数组末尾标号
//将有序的SR[i...m]和SR[m+1...n]归并为有序的TR[i...n]
void Merge(int SR[],int TR[],int i,int m,int n){
int j,k,l;
//j标记SR[m+1...n] 此时SR[m+1...n]是有序的
//i标记SR[i...m] 此时SR[i...m]也是有序的
//k标记TR
for(j=m+1,k=i;i<=m&&j<=n;k++){ //将SR中记录由小到大归并入TR
if(SR[i-1]<SR[j-1]){
TR[k-1]=SR[i-1];
i++;
}else{
TR[k-1]=SR[j-1];
j++;
}
}
if(i<=m){ //將剩余的SR[i...m]复制到TR中
for(l=i;l<=m;l++){
TR[k-1]=SR[l-1];
k++;
}
}
if(j<=n){ //將剩余的SR[m+1...n]复制到TR中
for(l=j;l<=n;l++){
TR[k-1]=SR[l-1];
k++;
}
}
}
//s为数组开始标号 t为数组末尾标号
//将SR[s...t]归并为TR1[s...t]
void MergeSort(int SR[],int TR1[],int s,int t){
int m;
int TR2[MAXSIZE];
if(s==t)
TR1[s-1]=SR[s-1];
else{
m=(s+t)/2; //将SR[s...t]平分为SR[s...m]和SR[m...t]
MergeSort(SR,TR2,s,m); //递归将SR[s...m]归并为有序TR2[s...m]
MergeSort(SR,TR2,m+1,t); //递归将SR[m+1...t]归并为有序TR2[m+1...t]
Merge(TR2,TR1,s,m,t); //将TR2[s...m]和TR2[m+1...t]归并到TR1[s...t]
}
}
int main(){
SqList *L=(SqList*)malloc(sizeof(SqList));
L->lengh=9;
L->r[0]=50;
L->r[1]=10;
L->r[2]=90;
L->r[3]=30;
L->r[4]=70;
L->r[5]=40;
L->r[6]=80;
L->r[7]=60;
L->r[8]=20;
MergeSort(L->r,L->r,1,L->lengh);
print(L);
system("pause");
}
归并排序复杂度分析
一趟归并需要将SR[1]~SR[n]中相邻的长度为h的有序序列进行两两归并,并将结果存放到TR1[1]~TR1[n]中,这需要将待排序序列中的所有记录扫描一遍,因此耗费O(n)时间,而由二叉树的深度可知,整个归并排序需要进行[log2n]次,因此,总的时间复杂度为O(nlogn),而且这是归并排序算法中最好、最坏、平均的时间性能。
由于归并排序在归并过程中需要与原始记录序列同样数量的存储空间存放归并结果以及递归深度为log2n的栈空间,因此空间复杂度为O(n+logn)。
归并排序需要两两比较,不存在跳跃,因此归并排序是一种稳定的排序算法,同时也是一种比较占用内存的算法。