关系代数的概述

数据模型不仅仅涉及用来描述数据的结构，它同时也需要一种操作这些数据的方法，使用户可以对数据进行查询和修改。为了开始学习关系上的数据操作，首先要引入一种专门的代数—关系代数。

传统关系代数的操作主要有以下四类：

1.通常的关系操作：并、交、差；

2.除去某些行或者列的操作，“选择”是获取（消除）某些行（元组）的操作，而“投影”是获取（“消除”）某些列的操作。

3.组合两个关系元组的操作。包括“笛卡儿积运算”，该操作尝试两个关系的所有可能的元组的配对方式，形成一个关系作为结果。另外还有许多“连接”（join）操作，它是从两个关系中选择一些元组配对。

4.“重命名”（renaming）操作。不影响关系中的元组，但是它改变了关系模式，即属性的名称或者是关系本身的名称被改变。

人们一般把关系代数的表达式称为查询（query）。

关系上的集合操作

三个最常用的集合操作是：并（union）、交（intersection）、差（difference）。

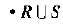
表示关系R和S的并，所得到的结果关系的元素是来自R或者S，又或者在R和S中都出现过。

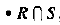
表示关系R和S的交，就是同时在R和S中存在的元素的集合。

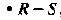
是关系R和S的差，它是由在R中出现但是不在S中出现的元素构成的集合。但是应当注意：S-R和R-S不同，前者表示由在S中出现但是不在R中出现的元素构成的集合。

当在关系上应用这些操作的时候，需要对关系R和S附加一些条件：

1.R和S必须是具有同样属性集合的表，同时，R和S的各个属性的类型（域）也必须匹配。

2.在做相应的集合操作（指并、交、差）之前，R和S的列必须经过排序，这样 保证它们的属性序对于两个关系来说完全相同。

例如存在如下两个关系R和S：

则它们的并运算的结果是：

交运算的结果是：

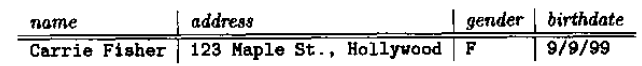
R-S的运算结果是：

投影

投影操作用来从关系R生成一个新的关系，这个关系只包含原来关系R中的部分列。比如关系Movies：

投影到关系的前三个属性的表达式是：

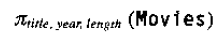
所得的结果是：

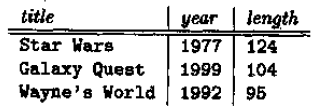
利用表达式：

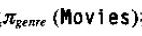
投影到属性genre，结果是一个单列关系：

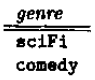
选择

当选择（selection）操作符应用到关系R上时，产生一个关系R的元组的子集合。结果关系的元组必须满足某个涉及R中属性的条件C，这个操作表示为：

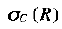
C是某个类型的条件表达式，它与人们熟悉的程序设计语言条件表达式类似，例如：C语言或者Java语言中的if关键字后面的条件表达式。所不同的是C中的操作数要么是一个常数，要么是一个属性。假设t是R中任意一个元组，把t代入到条件C中，如果代入的结果为真，那么这个元组就是选择结果中的一个元组，否则此元组不在结果中出现。

比如在关系Movies中，表达式：

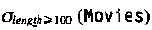
它的结果是：

第一、二个元组满足表达式length大于等于100，因此包括在结果中。

在关系Movies中选择所有Fox公司出品的至少有100分钟长的电影，就必须使用更加复杂、包含AND和两个子条件的表达式来实现这样的查询。这个表达式可以写成：

结果为：

笛卡儿积

关系R和S的笛卡儿积是一个有序对的集合，有序对的第一个元素是关系R中的任何一个元组，第二个元素是关系S中的任何一个元组，表示RxS。在习惯中关系R中的属性出现在关系S的属性的前面。

如果属性A在关系R和S中均出现，则结果关系模式中分别用R.A和S.A表示来自R和S的属性。

例如：

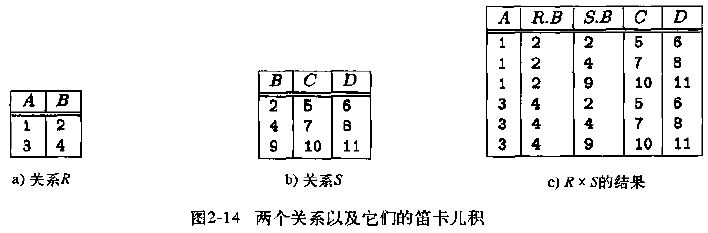
自然连接

和积相比，人们更经常对两个关系做连接（join）操作，连接时相应的元组必须在某些方面一致。最简单的就是所谓的自然链接。关系R和S的自然连接表示为：

此操作仅仅把在R和S模式中有某些共同属性，且此属性有相同的值得元组配对。我们把自然连接结果的元组称为连接元组。

图2-14a和b中关系R和S的自然连接结果是：

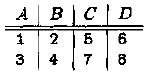
在一个连接当中，如果一个元组不能和另外关系中任何一个元组配对的话，这个元组就被称为悬浮元组。

在下面图2-16中，有另外两个关系U和V，它们的关系模式有共同的属性B和C，只有在属性B和C上一致的元组才能配对成功：

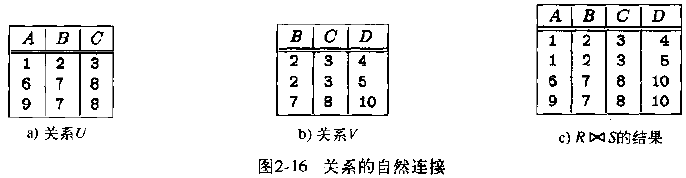
theta连接

自然连接必须根据某些特定的条件来把元组配对，虽然相等的公共属性是关系连接最常见的基础。但是人们有时候需要将满足其他条件的元组配对。为此就有了theta连接操作，历史上theta是指任意条件，但现在一般用C而不是theta表示这个条件。

关系R和关系S满足条件C的theta连接可以这样用符号来表示：

这个操作的结果是这样构造的：

1.先得到R和S的积；

2.在得到的关系中寻找满足条件C的元组；

比如在图2-16中考虑这样的操作：

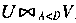
结果：

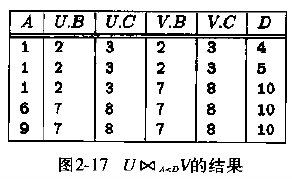
又例如操作：

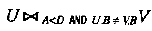
结果：

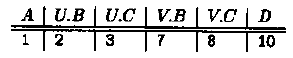
组合操作构成查询

考虑Movies关系，假设人们想知道“由Fox制作的至少100分钟的电影名称（title）和制作年份（year）”，计算该查询的一种方法是：

1.选择length大于等于100分钟的Movies关系中的元组；

2.选择studioName=‘Fox’的Movies元组；

3.计算（1）和（2）两个查询结果的交集。

4.把（3）得到的关系投影到title和year属性上。

这样的步骤可以用表达式数来表示。表达式树的计算是从下向上，内部结点上操作符的参量是其子树的结果。由于是自下而上计算，因此其子树的参量是可用的。

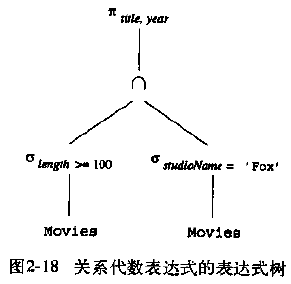
习惯上常选用线性符号来表示同样的表达式：

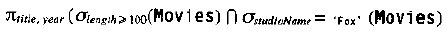
同一个计算可以用多个不同关系的代数表达式来描述，上面的查询可用用逻辑AND操作来替换“交”：