Aris

堆排序算法

2015/06/20 数据结构

数据结构堆的基本概念

堆是一种完全二叉树的数据结构。

堆具有完全二叉树的性质：每个结点的值都大于或等于其左右孩子结点的值，称之为大顶堆（如下图的左图）；每个结点的值都小于或等于其左右孩子结点的值，称之为小顶堆。

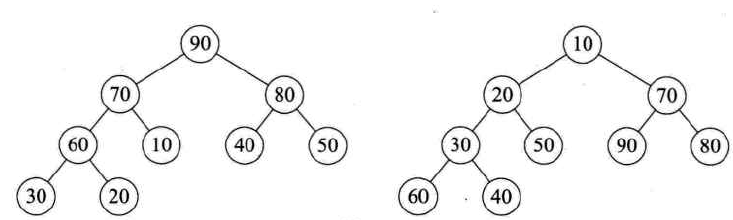
如果按照层序遍历的方式给结点从1开始编号，则结点之间满足如下关系：

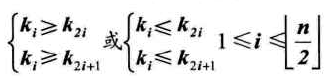
这里也用到完全二叉树的性质，如果i=1，则结点i是二叉树的根，无双亲；日过i>1，则双亲是结点[i/2]。如果一颗二叉树有n个几点，下标为i的结点，当2i<n时，2i是结点i的左孩子，2i+1是结点i的右孩子。

如下图，把大顶堆和小顶堆用层序遍历存入数组，则一定满足上面的关系表达：

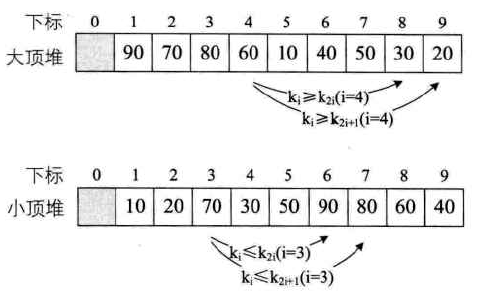
堆排序算法原理

假设我们排序的序列是（50，10，90，30，70，40，80，60，20），第一步先把这个序列构造成大顶堆。因此我们必须找到有孩子的的结点，规律是：序列长度为9，则9/2=4，因此标号1到4的结点都是有孩子的结点，如图所示：

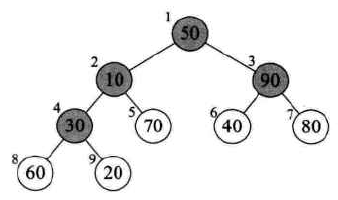
所谓的将待排序序列构建成为一个大顶堆，其实就是从下往上，从右到左，将每个非叶子结点当作根结点，将其和其子树调整成大顶堆。也就是按照4->3->2->1的结点顺序进行调整。

首先是结点4,结点4和左右孩子比较，小于其左右孩子中的最大的结点则交换，如下图所示，结点4左右孩子最大结点是结点8，因此发生交换：

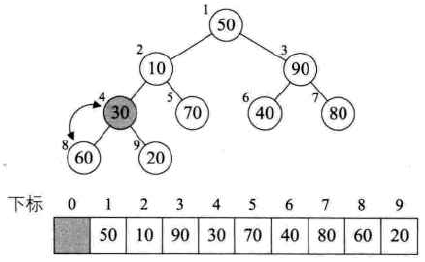
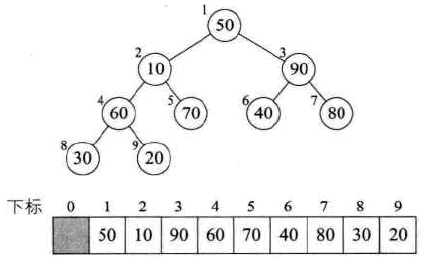
结点3的值比其左右孩子都大，满足大顶堆的条件，不需要调整。

然后调整结点2：

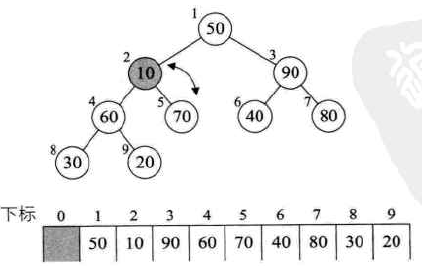
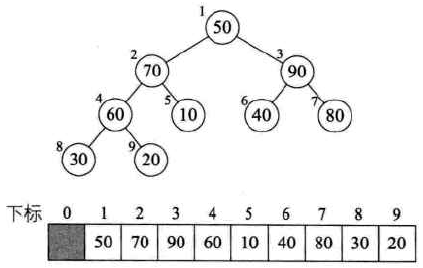
最后调整结点1：

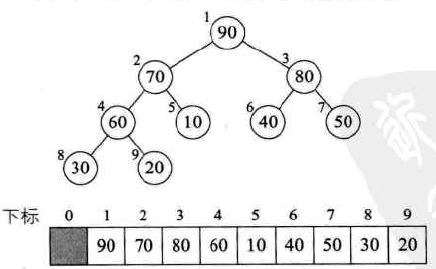
到目前为止，我们已经完成构建大顶堆的过程。

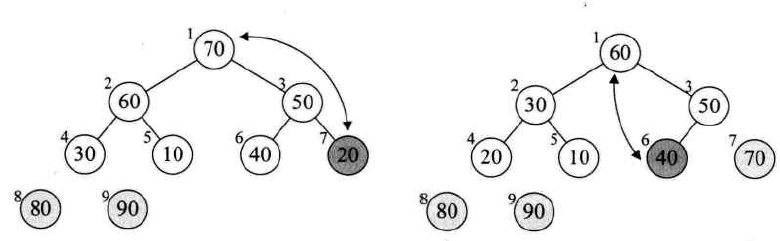
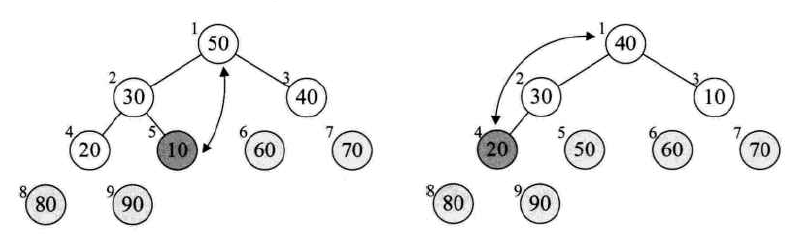
此时，堆定点的结点是序列中的最大值，把堆顶点的值和序列中最后的一个值做交换，可以得到最大值。这时剩下序列的长度减1。因为剩下的序列构不成大顶堆，因此必须重新调整，使其成为大顶堆。仔细观察，其实只有堆顶点的结点不满足大顶堆条件，其他顶点均满足，因此只需调整堆顶点即可：

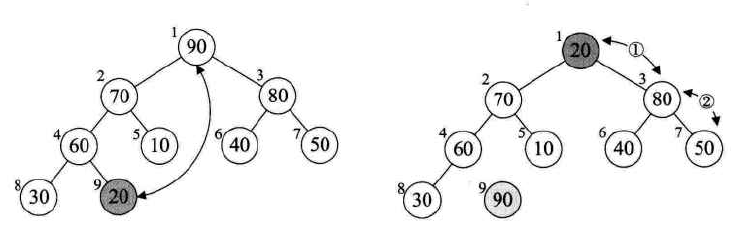
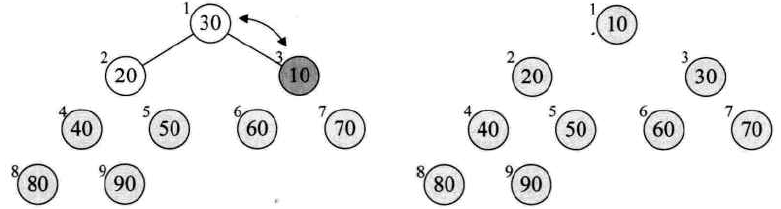
调整完以后，堆顶点又是最大值，又与剩余序列中最后一个结点交换，得到次大值点。如此循环下去，即可得到有序序列：

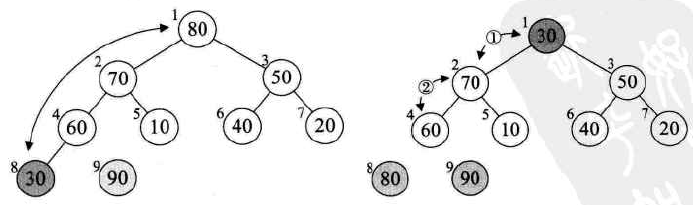
堆排序复杂度分析

堆排序的运行时间主要是消耗在初始构建堆和在重建堆时的反复筛选上。在构建堆的过程中，因为我们是从完全二叉树最下层最右边的非叶子结点开始构建，将它与其孩子进行比较，若有必要的互换，对于每个非叶子节点来说，其实最多进行两次比较和互换操作，因此整个构建堆的时间复杂度为O(n)。

在正式排序时，第i次取堆记录重建堆需要用O(log(i))的时间（完全二叉树的某个结点到根结点的距离为[log(i)]+1，并且需要取n-1次堆顶记录，因此重建的时间复杂度为O(nlogn)。由于堆排序对原始记录的排序状态并不敏感，因此它无论是最好、最坏和平均时间复杂度均为O(nlogn)。这在性能上显然要远远好过于冒泡、简单选择、直接插入的O(n2)的时间复杂度。在空间复杂度上，它只有一个用来交换的暂存单元，也非常不错的。不过由于记录的比较与交换是跳跃进行，因此堆排序也是一种不稳定的排序方法。

由于初始构建堆需要比较的次数较多，因此，它并不适合待排序序列个数较少的情况。堆排序是简单选择排序的改进。

堆排序完整程序代码

#include <iostream>

using namespace std;

#define MAXSIZE 10                  //用于排序数组个数最大值 可根据需要修改
typedef struct{
	int r[MAXSIZE];                 //数组
	int lengh;                      //数组的实际长度
}SqList;

void swap(SqList *L,int i,int j){   //对数组的交换操作
	int temp=L->r[i];
	L->r[i]=L->r[j];
	L->r[j]=temp;
}

void print(SqList *L){              //打印数组
	for(int i=0;i<L->lengh;i++){
		cout<<L->r[i]<<" ";
	}
	cout<<endl;
}

void HeapAdjust(SqList *L,int s,int m){   //给长度为m的数组L中标号为s的结点进行调整 使其满足大顶堆条件
	int temp=L->r[s-1];                   //先保存当前结点
	for(int j=2*s;j<=m;j=2*j){            //2*s表示结点s的左孩子
		if(j<m){                          //j小于m 表明s还有右孩子
			if(L->r[j-1]<L->r[j])         //比较左孩子和右孩子的大小 选出最大的一个
				j++;                      //如果右孩子比较大 标号j指向右孩子
		}

		if(temp>L->r[j-1])                //如果temp比左孩子和右孩子都大
			break;                        //则该结点已经满足大顶堆条件 跳出该循环
		else{
			L->r[s-1]=L->r[j-1];          //否则发生交换
			s=j;
		}
	}
	L->r[s-1]=temp;                       //原始结点s的值temp交换完成
}


void HeapSort(SqList *L){           //对顺序表L进行堆排序
	for(int i=L->lengh/2;i>0;i--)   //首先找到非叶子结点 自下而上进行调整 使之满足大顶堆条件
		HeapAdjust(L,i,L->lengh);   //该循环运行完成以后 数组L就是一个大顶堆
	                                //i表示标号为i的结点进行大顶堆调整
	for(int i=L->lengh;i>1;i--){
		swap(L,0,i-1);              //将堆顶记录和当前未经排序子序列的最后一个记录交换
		HeapAdjust(L,1,i-1);        //交换以后 剩下堆顶不满足大顶堆条件 因此调整堆顶结点
	}
}


int main(){
	SqList *L=(SqList*)malloc(sizeof(SqList));
	L->lengh=9;
	L->r[0]=50;
	L->r[1]=10;
	L->r[2]=90;
	L->r[3]=30;
	L->r[4]=70;
	L->r[5]=40;
	L->r[6]=80;
	L->r[7]=60;
	L->r[8]=20;
	print(L);
	cout<<"堆排序以后："<<endl;
	HeapSort(L);
	print(L);
	system("pause");
}

程序运行结果：

Search

    Post Directory