希尔排序的实质就是分组插入排序,该方法又称缩小增量排序,因DL.Shell于1959年提出而得名。
该方法的基本思想是:先将整个待排元素序列分割成若干个子序列(由相隔某个“增量”的元素组成的)分别进行直接插入排序,然后依次缩减增量再进行排序,待整个序列中的元素基本有序(增量足够小)时,再对全体元素进行一次直接插入排序。因为直接插入排序在元素基本有序的情况下(接近最好情况),效率是很高的,因此希尔排序在时间效率上比前两种方法有较大提高。
要编写希尔排序,首先要编写直接插入排序:
#include <iostream>
using namespace std;
#define MAXSIZE 10 //用于排序数组个数最大值 可根据需要修改
typedef struct{
int r[MAXSIZE]; //数组
int lengh; //数组的实际长度
}SqList;
void print(SqList *L){
for(int i=0;i<L->lengh;i++){
cout<<L->r[i]<<" ";
}
cout<<endl;
}
void InsertSort(SqList *L){
for(int i=1;i<L->lengh;i++){
if(L->r[i]<L->r[i-1]){ //判断是否需要移动
int j;
for(j=i-1;j>=0;j--){ //确定插入位置j
if(L->r[i]>L->r[j])
break;
}
int temp=L->r[i]; //保存插入元素
for(int x=i;x>j+1;x--){ //元素往后退
L->r[x]=L->r[x-1];
}
L->r[j+1]=temp; //插入元素
}
}
}
int main(){
SqList *L=(SqList*)malloc(sizeof(SqList));
L->lengh=10;
L->r[0]=49;
L->r[1]=38;
L->r[2]=65;
L->r[3]=97;
L->r[4]=26;
L->r[5]=13;
L->r[6]=27;
L->r[7]=49;
L->r[8]=55;
L->r[9]=4;
print(L);
InsertSort(L);
print(L);
system("pause");
}
程序运行结果:
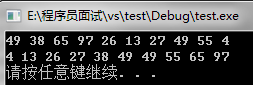
以n=10的一个数组49, 38, 65, 97, 26, 13, 27, 49, 55, 4为例
第一次增量 incr = 10/2 = 5:
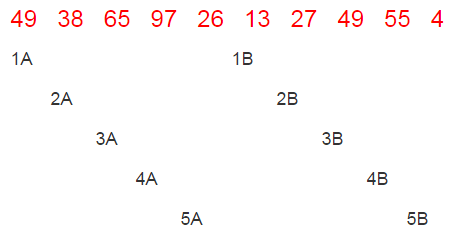
1A,1B,2A,2B等为分组标记,数字相同的表示在同一组,大写字母表示是该组的第几个元素,每次对同一组的数据进行直接插入排序。即分成了五组(49, 13) (38, 27) (65, 49) (97, 55) (26, 4)这样每组排序后就变成了(13, 49) (27, 38) (49, 65) (55, 97) (4, 26)。
#include <iostream>
using namespace std;
#define MAXSIZE 10 //用于排序数组个数最大值 可根据需要修改
typedef struct{
int r[MAXSIZE]; //数组
int lengh; //数组的实际长度
}SqList;
void print(SqList *L){
for(int i=0;i<L->lengh;i++){
cout<<L->r[i]<<" ";
}
cout<<endl;
}
void InsertSort2(SqList *L){
int incr=5;
for(int ii=0;ii<incr;ii++){ //外围循环 增量是多少 就循环多少次
for(int i=ii+incr;i<L->lengh;i=i+incr){ //内围循环 由直接排序改进而来 把增量1改为incr
if(L->r[i]<L->r[i-incr]){ //判断是否需要移动
int j;
for(j=i-incr;j>=0;j=j-incr){ //确定插入位置j
if(L->r[i]>L->r[j])
break;
}
int temp=L->r[i]; //保存插入元素
for(int x=i;x>j+incr;x=x-incr){ //元素往后退
L->r[x]=L->r[x-incr];
}
L->r[j+incr]=temp;
}
}
}
}
int main(){
SqList *L=(SqList*)malloc(sizeof(SqList));
L->lengh=10;
L->r[0]=49;
L->r[1]=38;
L->r[2]=65;
L->r[3]=97;
L->r[4]=26;
L->r[5]=13;
L->r[6]=27;
L->r[7]=49;
L->r[8]=55;
L->r[9]=4;
print(L);
InsertSort2(L);
print(L);
system("pause");
}
程序运行结果:
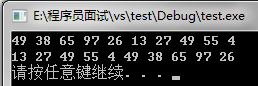
第二次 incr = 5/2 = 2
#include <iostream>
using namespace std;
#define MAXSIZE 10 //用于排序数组个数最大值 可根据需要修改
typedef struct{
int r[MAXSIZE]; //数组
int lengh; //数组的实际长度
}SqList;
void print(SqList *L){
for(int i=0;i<L->lengh;i++){
cout<<L->r[i]<<" ";
}
cout<<endl;
}
void InsertSort2(SqList *L){
int incr=5;
for(int ii=0;ii<incr;ii++){ //外围循环 增量是多少 就循环多少次
for(int i=ii+incr;i<L->lengh;i=i+incr){ //内围循环 由直接排序改进而来 把增量1改为incr
if(L->r[i]<L->r[i-incr]){ //判断是否需要移动
int j;
for(j=i-incr;j>=0;j=j-incr){ //确定插入位置j
if(L->r[i]>L->r[j])
break;
}
int temp=L->r[i]; //保存插入元素
for(int x=i;x>j+incr;x=x-incr){ //元素往后退
L->r[x]=L->r[x-incr];
}
L->r[j+incr]=temp;
}
}
}
incr=2;
for(int ii=0;ii<incr;ii++){ //外围循环 增量是多少 就循环多少次
for(int i=ii+incr;i<L->lengh;i=i+incr){ //内围循环 由直接排序改进而来
if(L->r[i]<L->r[i-incr]){ //判断是否需要移动
int j;
for(j=i-incr;j>=0;j=j-incr){ //确定插入位置j
if(L->r[i]>L->r[j])
break;
}
int temp=L->r[i]; //保存插入元素
for(int x=i;x>j+incr;x=x-incr){ //元素往后退
L->r[x]=L->r[x-incr];
}
L->r[j+incr]=temp;
}
}
}
}
int main(){
SqList *L=(SqList*)malloc(sizeof(SqList));
L->lengh=10;
L->r[0]=49;
L->r[1]=38;
L->r[2]=65;
L->r[3]=97;
L->r[4]=26;
L->r[5]=13;
L->r[6]=27;
L->r[7]=49;
L->r[8]=55;
L->r[9]=4;
print(L);
InsertSort2(L);
print(L);
system("pause");
}
程序运行结果:
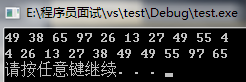
第三次 incr = 2/2 = 1

#include <iostream>
using namespace std;
#define MAXSIZE 10 //用于排序数组个数最大值 可根据需要修改
typedef struct{
int r[MAXSIZE]; //数组
int lengh; //数组的实际长度
}SqList;
void print(SqList *L){
for(int i=0;i<L->lengh;i++){
cout<<L->r[i]<<" ";
}
cout<<endl;
}
void InsertSort2(SqList *L){
int incr=5;
for(int ii=0;ii<incr;ii++){ //外围循环 增量是多少 就循环多少次
for(int i=ii+incr;i<L->lengh;i=i+incr){ //内围循环 由直接排序改进而来 把增量1改为incr
if(L->r[i]<L->r[i-incr]){ //判断是否需要移动
int j;
for(j=i-incr;j>=0;j=j-incr){ //确定插入位置j
if(L->r[i]>L->r[j])
break;
}
int temp=L->r[i]; //保存插入元素
for(int x=i;x>j+incr;x=x-incr){ //元素往后退
L->r[x]=L->r[x-incr];
}
L->r[j+incr]=temp;
}
}
}
incr=2;
for(int ii=0;ii<incr;ii++){ //外围循环 增量是多少 就循环多少次
for(int i=ii+incr;i<L->lengh;i=i+incr){ //内围循环 由直接排序改进而来
if(L->r[i]<L->r[i-incr]){ //判断是否需要移动
int j;
for(j=i-incr;j>=0;j=j-incr){ //确定插入位置j
if(L->r[i]>L->r[j])
break;
}
int temp=L->r[i]; //保存插入元素
for(int x=i;x>j+incr;x=x-incr){ //元素往后退
L->r[x]=L->r[x-incr];
}
L->r[j+incr]=temp;
}
}
}
incr=1;
for(int ii=0;ii<incr;ii++){ //外围循环 增量是多少 就循环多少次
for(int i=ii+incr;i<L->lengh;i=i+incr){ //内围循环 由直接排序改进而来
if(L->r[i]<L->r[i-incr]){ //判断是否需要移动
int j;
for(j=i-incr;j>=0;j=j-incr){ //确定插入位置j
if(L->r[i]>L->r[j])
break;
}
int temp=L->r[i]; //保存插入元素
for(int x=i;x>j+incr;x=x-incr){ //元素往后退
L->r[x]=L->r[x-incr];
}
L->r[j+incr]=temp;
}
}
}
}
int main(){
SqList *L=(SqList*)malloc(sizeof(SqList));
L->lengh=10;
L->r[0]=49;
L->r[1]=38;
L->r[2]=65;
L->r[3]=97;
L->r[4]=26;
L->r[5]=13;
L->r[6]=27;
L->r[7]=49;
L->r[8]=55;
L->r[9]=4;
print(L);
InsertSort2(L);
print(L);
system("pause");
}
程序运行结果:
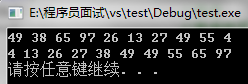
完整的希尔排序代码:
#include <iostream>
using namespace std;
#define MAXSIZE 10 //用于排序数组个数最大值 可根据需要修改
typedef struct{
int r[MAXSIZE]; //数组
int lengh; //数组的实际长度
}SqList;
void print(SqList *L){
for(int i=0;i<L->lengh;i++){
cout<<L->r[i]<<" ";
}
cout<<endl;
}
void ShellSort(SqList *L){
int incr=5;
do{
for(int ii=0;ii<incr;ii++){ //外围循环 增量是多少 就循环多少次
for(int i=ii+incr;i<L->lengh;i=i+incr){ //内围循环 由直接排序改进而来 把增量1改为incr
if(L->r[i]<L->r[i-incr]){ //判断是否需要移动
int j;
for(j=i-incr;j>=0;j=j-incr){ //确定插入位置j
if(L->r[i]>L->r[j])
break;
}
int temp=L->r[i]; //保存插入元素
for(int x=i;x>j+incr;x=x-incr){ //元素往后退
L->r[x]=L->r[x-incr];
}
L->r[j+incr]=temp;
}
}
}
incr=incr/2;
}while(incr!=0);
}
int main(){
SqList *L=(SqList*)malloc(sizeof(SqList));
L->lengh=10;
L->r[0]=49;
L->r[1]=38;
L->r[2]=65;
L->r[3]=97;
L->r[4]=26;
L->r[5]=13;
L->r[6]=27;
L->r[7]=49;
L->r[8]=55;
L->r[9]=4;
print(L);
ShellSort(L);
print(L);
system("pause");
}
希尔排序的时间复杂度为O(n3/2),要好于直接排序的O(n2)。
最好情况:由于希尔排序的好坏和步长d的选择有很多关系,因此,目前还没有得出最好的步长如何选择(现在有些比较好的选择了,但不确定是否是最好的)。所以,不知道最好的情况下的算法时间复杂度。
最坏情况下:O(N*logN),最坏的情况下和平均情况下差不多。
平均情况下:O(N*logN)
稳定性:由于多次插入排序,我们知道一次插入排序是稳定的,不会改变相同元素的相对顺序,但在不同的插入排序过程中,相同的元素可能在各自的插入排序中移动,最后其稳定性就会被打乱,所以shell排序是不稳定的。(有个猜测,方便记忆:一般来说,若存在不相邻元素间交换,则很可能是不稳定的排序。)