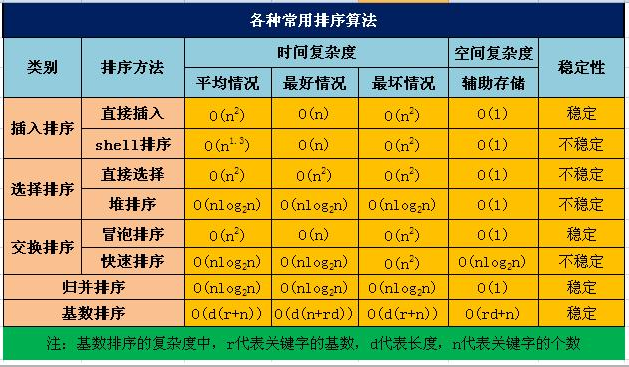
排序用到的结构与函数
#define MAXSIZE 10 //用于排序数组个数最大值 可根据需要修改
typedef struct{
int r[MAXSIZE]; //数组
int lengh; //数组的实际长度
}SqList;
冒泡排序
冒泡排序实现
冒泡排序是一种交换排序,它的基本思想是:两两比较相邻记录的关键字,如果反序则交换,直到没有反序的记录为止。
如图,通过无序区中相邻记录关键字间的比较和位置的交换,使关键字最小的记录如气泡一般逐渐往上“漂浮”直至“水面”。
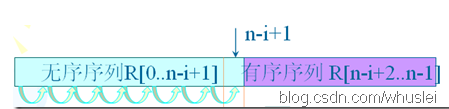
完整程序:
#include <iostream>
using namespace std;
#define MAXSIZE 10 //用于排序数组个数最大值 可根据需要修改
typedef struct{
int r[MAXSIZE]; //数组
int lengh; //数组的实际长度
}SqList;
void swap(SqList *L,int i,int j){ //对数组的交换操作
int temp=L->r[i];
L->r[i]=L->r[j];
L->r[j]=temp;
}
void print(SqList *L){
for(int i=0;i<L->lengh;i++){
cout<<L->r[i]<<" ";
}
cout<<endl;
}
void BubleSort(SqList *L){
for(int i=0;i<L->lengh-1;i++){
for(int j=0;j<L->lengh-1-i;j++){
if(L->r[j]<L->r[j+1])
swap(L,j,j+1);
}
}
}
int main(){
SqList *L=(SqList*)malloc(sizeof(SqList));
L->lengh=5;
L->r[0]=5;
L->r[1]=2;
L->r[2]=4;
L->r[3]=7;
L->r[4]=1;
print(L);
BubleSort(L);
print(L);
system("pause");
}
冒泡排序时间复杂度分析
冒泡排序时间复杂度主要在于比较和交换。假设有n个元素,第一个元素比较n-1次,第二个元素比较n-2次,….3次,2次和1次。
一共为:
1+2+3+…n-1=(n-1+1)*(n-1)/2=(n-1)*n/2次
所以时间复杂度为O(n2)。在最差的情况下,交换次数也为(n-1)*n/2次。
最好情况下:正序有序,则只需要比较n次。故为O(n)
最坏情况下:逆序有序,则需要比较(n-1)+(n-2)+…+1,故为O(n*n)
稳定性:排序过程中只交换相邻两个元素的位置。因此,当两个数相等时,是没必要交换两个数的位置的。所以,它们的相对位置并没有改变,冒泡排序算法是稳定的!
改进的冒泡排序
按照上面的算法,如果序列已经有序,但是算法任然不依不挠地全部比较一下,尽管没有交换数据,但是之后的大量比较还是大大地多余了。
改进算法:
void BubleSort(SqList *L){
bool flag=true; //flag用来作为标记
for(int i=0;i<L->lengh-1&&flag;i++){ //如果flag为true 则退出循环
flag=false;
for(int j=0;j<L->lengh-1-i;j++){
if(L->r[j]<L->r[j+1]){
swap(L,j,j+1);
flag=true; //如果有交换 flag为true
}
}
}
}
选择排序
冒泡排序的思想就是不断地在交换,通过交换完成最终的排序。选择排序就是在排序时找到合适的关键字再做交换,并且只移动一次就完成相应关键字的排序定位工作。
简单选择排序算法就是通过n-1次关键字之间的比较,从n-i+1个记录中选出关键字最小的记录,并和第i(1=<i<=n)个记录交换之。
实现代码:
#include <iostream>
using namespace std;
#define MAXSIZE 10 //用于排序数组个数最大值 可根据需要修改
typedef struct{
int r[MAXSIZE]; //数组
int lengh; //数组的实际长度
}SqList;
void swap(SqList *L,int i,int j){ //对数组的交换操作
int temp=L->r[i];
L->r[i]=L->r[j];
L->r[j]=temp;
}
void print(SqList *L){
for(int i=0;i<L->lengh;i++){
cout<<L->r[i]<<" ";
}
cout<<endl;
}
void SelectSort(SqList *L){
for(int i=0;i<L->lengh-1;i++){
int max=L->r[i];
int b=i;
for(int j=i+1;j<L->lengh;j++){
if(max<L->r[j]){
max=L->r[j];
b=j;
}
}
if(b!=i) //如果b发生了改变 就交换
swap(L,i,b);
}
}
int main(){
SqList *L=(SqList*)malloc(sizeof(SqList));
L->lengh=5;
L->r[0]=5;
L->r[1]=2;
L->r[2]=4;
L->r[3]=7;
L->r[4]=1;
print(L);
SelectSort(L);
print(L);
system("pause");
}
时间复杂度分析:
从简单选择排序的过程来看,和冒泡排序比较,它最大的特点就是交换一定数据次数减少,这样也就节约了相应的时间。分析它的时间复杂度发现,无论最好还是最差的情况,其比较次数都是一样多。
第i趟排序需要进行n-i次关键字的比较,此时需要比较:
1+2+3…+n-2+n-1=n*(n-1)/2次
最好情况下:交换0次,但是每次都要找到最小的元素,因此大约必须遍历NN次,因此为O(NN)。减少了交换次数!最坏情况下,平均情况下:O(N*N)
而对于交换次数而言,当最好的时候,交换次数为0次,最差的时候,也就是初始降序时,交换次数为n-1次,基于最终的排序时间是比较与交换的次数总和,因此,总的时间复杂度依然为O(n2)。尽管和冒泡排序算法时间复杂度相同,但是简单选择排序的性能还是略优于冒泡排序。
稳定性:由于每次都是选取未排序序列A中的最小元素x与A中的第一个元素交换,因此跨距离了,很可能破坏了元素间的相对位置,因此选择排序是不稳定的!
直接插入排序
直接插入排序(Straight Insertion Sort)的基本操作是将一个记录插入到已经排序号的有序表中,从而得到一个新的、记录数增1的有序表。
代码实现:
#include <iostream>
using namespace std;
#define MAXSIZE 10 //用于排序数组个数最大值 可根据需要修改
typedef struct{
int r[MAXSIZE]; //数组
int lengh; //数组的实际长度
}SqList;
void swap(SqList *L,int i,int j){ //对数组的交换操作
int temp=L->r[i];
L->r[i]=L->r[j];
L->r[j]=temp;
}
void print(SqList *L){
for(int i=0;i<L->lengh;i++){
cout<<L->r[i]<<" ";
}
cout<<endl;
}
void InsertSort(SqList *L){
for(int i=1;i<L->lengh;i++){
int j=i;
while(j>=1){
if(L->r[j]>=L->r[j-1]){ //退出循环
break;
}else{
swap(L,j,j-1); //往前进行比较 不断进行交换后
}
j--;
}
}
}
void InsertSort2(SqList *L){
for(int i=1;i<L->lengh;i++){
int j=i;
while(j>=1){
if(L->r[i]>=L->r[j-1]){ //退出循环
break;
}
j--;
}
int temp=L->r[i]; //保存要插入的值
for(int x=i;x>j;x--){ //每个数据都往后退
L->r[x]=L->r[x-1];
}
L->r[j]=temp; //插入值
}
}
int main(){
SqList *L=(SqList*)malloc(sizeof(SqList));
L->lengh=5;
L->r[0]=5;
L->r[1]=2;
L->r[2]=4;
L->r[3]=7;
L->r[4]=3;
print(L);
InsertSort2(L);
print(L);
system("pause");
}
直接插入排序算法复杂度分析:
从空间上来看,它只需需要一个记录的付诸空间,因此,关键是看它的时间复杂度。
当最好的情况,也就是要排序的表本身就是有序的,比如{2,3,4,5,6}
首先是比较次数:
3比较1次
4比较1次
5比较1次
6比较1次
所以一共比较n-1次,移动次数为0次,时间复杂度为O(n)。
最坏的情况是完全逆序:如{6,5,4,3,2}
首先是比较次数:
5比较1次
4比较2次
3比较3次
2比较4次
因此比较次数一共为:1+2+3+…+n-1=n*(n-1)/2次
然后是交换次数(包括中间值交换):
5:首先5赋值给中间值一次,6往后推一次,插入一次,共3次
4:首先4赋值给中间值一次,5、6往后推各一次,插入一次,共4次
3:共5次
2:共6次
一共交换次数为:3+4+…n+1=(n+4)*(n-1)/2
因此直接插入排序的时间复杂度为O(n*n)。
稳定性:就是有两个相同的元素,排序先后的相对位置是否变化,主要用在排序时有多个排序规则的情况下。在插入排序中,K1是已排序部分中的元素,当K2和K1比较时,直接插到K1的后面(没有必要插到K1的前面,这样做还需要移动!!),因此,插入排序是稳定的。