线索二叉树的原理
本节内容参考《大话数据结构》丛书。
二叉树的指针域并不都被充分利用,有很多空指针域的存在,这实在不是好现象,应到想办法利用起来。
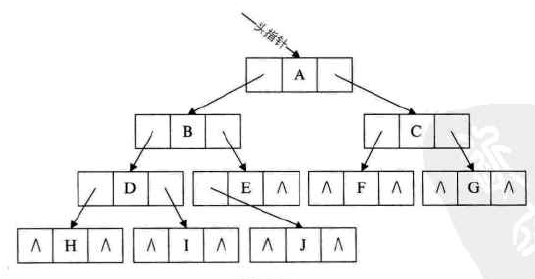
对于一个有n个节点的二叉链表,每个结点有指向左右孩子的两个指针,所以一共是2n个指针域。而n个节点的二叉树一共有n-1条分支线,也就是说其实存在2n-(n-1)=n+1个空指针域。这些空间不存储任何事物,白白的浪费着内存的资源。
另一方面,我们在做遍历时,我可以清楚的知道任意一个结点的前驱和后继是哪一个。如果不做遍历,仅仅在二叉链表上,我们只能知道每个结点指向其左右孩子结点的地址,而不知道某个结点的前驱是谁,后继是谁。要想知道,必须遍历一次。解决这个问题就是考虑在创建二叉树是就记住这些前驱和后继,从而节省时间。
因此,结合以上两个角度分析,我们可以利用那些空地址,存放指向结点在某种遍历次序下的前驱和后继结点的地址。就如同GPS导航仪一样,我们对目的地址的位置一无所知,但它每次都可以告诉我从当前位置的下一步应该走向哪里。
我们把这种指向前驱和后继的指针称为线索,加上线索的二叉链表称为线索链表,相应的二叉树就称为线索二叉树(Threaded Binary Three)。
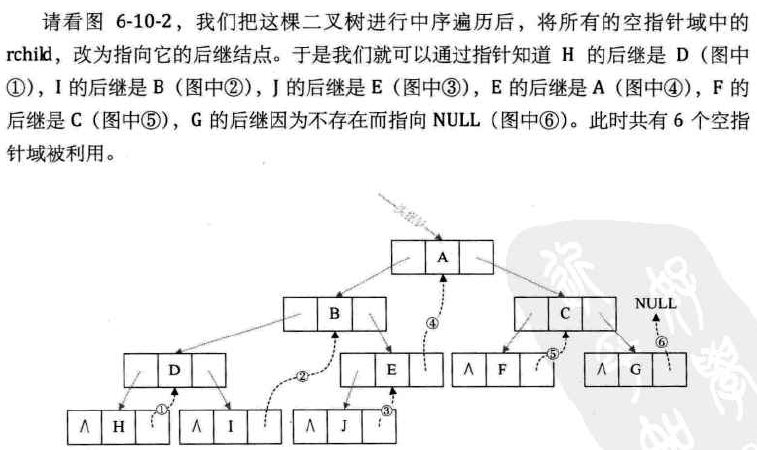
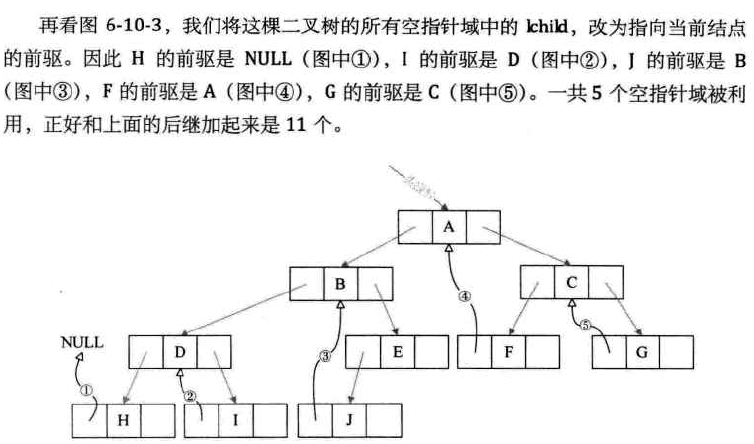
其实线索二叉树等于是把一颗二叉树转变成了一个双向链表,这样对我们的插入删除结点、查找某个结点都带来了方便。所以我们对二叉树以某种次序遍历使其变为线索二叉树的过程称做事线索化。
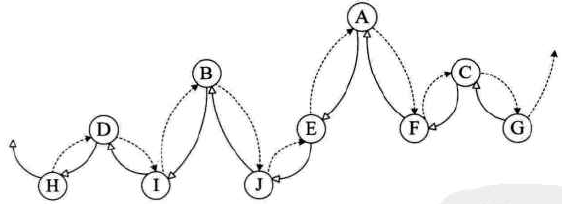
如何知道某一点的lchild是指向它的左孩子还是指向前驱?显然我们在决定lchild是指向左孩子还是前驱,rchild是指向右孩子还是前驱,需要一个区分标志。因此,我们在每个结点再增设两个标志域ltag和rtag,注意ltag和rtag只是存放0或1数字的布尔型变量,其占用的内存空间要小于lchild和rchild的指针变量。结点结构:

ltag为0时指向该结点的左孩子,为1时指向该结点的前驱;
rtag为0时指向该结点的右孩子,为1时指向该结点的后继;
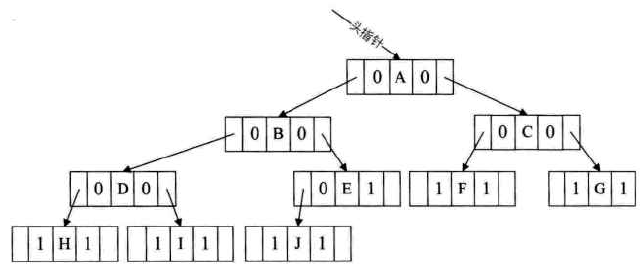
线索二叉树结构的实现
首先是二叉树的线索存储结构定义代码:
typedef enum {Link,Thread} PointerTag; //枚举变量 判断指向线索还是左右孩子
typedef struct BiThrNode{
int data;
struct BiThrNode *lchild;
struct BiThrNode *rchild;
PointerTag LTag;
PointerTag RTag;
}BiThrNode,*BiThrTree;
线索化的实质是将二叉树链表中的空指针改为指向前驱或者后继的线索。由于前驱和后继的信息只有在遍历二叉树时才能得到,所以线索二叉树的过程就是在遍历二叉树过程中修改空指针的过程。
中序遍历线索化的递归函数代码如下:
void InThreading(BiThrTree p){
if(p){
InThreading(p->lchild); //递归左子树线索化
if(!p->lchild){ //没有左孩子
p->LTag=Thread; //前驱线索
p->lchild=pre; //左孩子指针指向前驱
}
if(pre!=NULL){
if(!pre->rchild){ //前驱没有右孩子
pre->RTag=Thread; //后继线索
pre->rchild=p; //前驱右孩子指针指向后继(当前结点p)
}
}
pre=p; //保持pre指向p的前驱
InThreading(p->rchild); //递归右子树线索化
}
}
if(!p->lchid)表示如果结点的左指针域为空,要指向该结点的前驱,因为其前驱结点刚刚访问过,赋值给了pre,所以可将pre赋值给p->lchild,并修改p->LTag=Thread以完成前驱结点的线索化。
因为此时p结点的后继还没有访问到,因此只能对它的前驱结点pre的右指针rchild做判断,if(!p->rchild)表示如果为空,则p就是pre的后继,于是pre->rchild=p,并且设置pre->RTag=Thread,完成后继结点的线索化。
我们可以发现线索二叉树其实就等于操作一个双向链表结构。和双向链表结构一样,在二叉树线索链表上添加一个头结点,并令其lchild域的指针指向二叉树的根结点,其rchild域的指针指向中序遍历时访问的最后一个结点。这样定义的好处就是我们既可以从第一个结点起顺后继进行遍历,也可以从最后一个结点起顺前驱进行遍历。

遍历代码:
void InOrderTraverse_Thr(BiThrTree T){
BiThrTree p;
p=T->lchild; //p指向根节点
while(p!=T){ //空树或遍历结束时 p==T
while(p->LTag==Link) //当LTag==0时循环到中序序列第一个结点
p=p->lchild;
printf("%d",p->data); //显示结点数据 可以更改为其他对结点操作
while(p->RTag==Thread && p->rchild!=T){
p=p->rchild;
printf("%d",p->data);
}
p=p->rchild; //p进至其右子树跟
}
}
代码解析:
p=T->lchild意思是让p指向根结点开始遍历。
while(p!=T)意思是循环直到p指向头结点,于是要T相等,因为T指向头结点,从而结束循环,否则将一直循环下去进行遍历操作。
while(p->LTag==Link)这个循环就是找到中序遍历的第一个结点后结束循环,因为中序遍历的第一个结点的LTag==Thread。
while(p->RTag==Tread && p->richild!=T)表示判断p的rlichild是否指向p的后继并且不是指向头结点,若是,则访问其后继结点并赋值p=p->rchild。
线索二叉树总结
线索二叉树充分利用了空指针域的空间,有保证了创建时得分一次遍历就可以终生受用前驱后继的信息。所以在实际问题中,如果所用的二叉树需经常遍历或查找结点时需要的某种遍历序列中的前驱和后继,那么采用线索二叉链表的存储结构就是非常不错的选择。
完整的程序代码
#include <iostream>
using namespace std;
typedef enum {Link,Thread} PointerTag; //枚举变量 判断指向线索还是左右孩子
typedef struct BiThrNode{
int data;
struct BiThrNode *lchild;
struct BiThrNode *rchild;
PointerTag LTag;
PointerTag RTag;
}BiThrNode,*BiThrTree;
BiThrTree pre=NULL; //全局变量 始终指向刚刚访问过的结点
void CreateBiThrTree(BiThrTree &T){ //创建二叉树
int num;
cin>>num;
if(num!=0){
T=(BiThrTree)malloc(sizeof(BiThrNode));
T->data=num;
T->LTag=Link;
T->RTag=Link;
CreateBiThrTree(T->lchild);
CreateBiThrTree(T->rchild);
}else{
T=NULL;
}
}
void PreOrderVist(BiThrTree T){ //递归先序遍历
if(T!=NULL){
cout<<T->data<<endl;
PreOrderVist(T->lchild);
PreOrderVist(T->rchild);
}
}
void InThreading(BiThrTree p){
if(p){
InThreading(p->lchild); //递归左子树线索化
if(!p->lchild){ //没有左孩子
p->LTag=Thread; //前驱线索
p->lchild=pre; //左孩子指针指向前驱
}
if(pre!=NULL){
if(!pre->rchild){ //前驱没有右孩子
pre->RTag=Thread; //后继线索
pre->rchild=p; //前驱右孩子指针指向后继(当前结点p)
}
}
pre=p; //保持pre指向p的前驱
InThreading(p->rchild); //递归右子树线索化
}
}
void ThreadingTree(BiThrTree &T){
InThreading(T); //中序线索化二叉树
BiThrTree H;
H=(BiThrTree)malloc(sizeof(BiThrNode)); //生成头结点
H->lchild=T;
T=H;
}
void InOrderTraverse_Thr(BiThrTree T){
BiThrTree p;
p=T->lchild; //p指向根节点
while(p!=T){ //空树或遍历结束时 p==T
while(p->LTag==Link) //当LTag==0时循环到中序序列第一个结点
p=p->lchild;
printf("%d",p->data); //显示结点数据 可以更改为其他对结点操作
while(p->RTag==Thread && p->rchild!=T){
p=p->rchild;
printf("%d",p->data);
}
p=p->rchild; //p进至其右子树跟
}
}
int main(){
BiThrTree T;
CreateBiThrTree(T);
PreOrderVist(T);
ThreadingTree(T);
InOrderTraverse_Thr(T);
system("pause");
}