数组一旦被定义,它的维数和维界就不再改变。
数组的顺序表示和实现
无论是几维的数组,最后在内存中的存储结构都是一维连续单元。
由于存储单元是一维结构,而数组是多维的结构,则用一组连续存储单元存放数组的数据元素就有个次序约定的问题。对二维数组可有两种存储方式:一种以列序为主序的存储方式;一种是以行序为主序的存储方式。
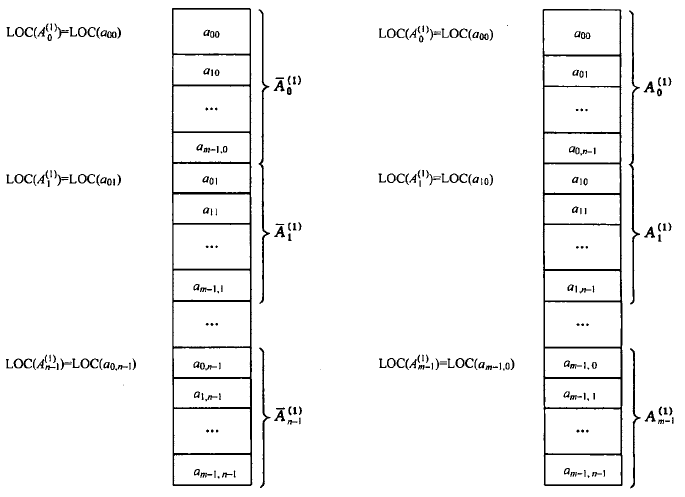

数组的顺序存储结构:
typedef struct{
ElemType *base;
int dim; //数组维数
int *bounds; //数组维界基址 存放每个维度的大小
int *constans; //数组映像函数常量基址
}Array;
关于constans:
假设对于一个四维的数组
每个维度大小为4 5 7 6,则有:
4 5 7 6
constans 5x7x6x1 7x6x1 6x1 1
完整代码:
#include <stdio.h>
#include <stdlib.h>
#include <stdarg.h>
#include <iostream>
#define MAX_ARRAY_DIM 8 //假设数组维数最大值为8
typedef int ElemType;
typedef int Status;
//函数结果状态代码
#define OK 1
#define ERROR 0
typedef struct{
ElemType *base;
int dim; //数组维数
int *bounds; //数组维界基址 存放每个维度的大小
int *constans; //数组映像函数常量基址
}Array;
//求元素A中相对地址
Status Locate(Array A,va_list ap,int &off){
off=0;
int ind;
for(int i=0;i<A.dim;i++){
ind=va_arg(ap,int);
if(ind<0||ind>=A.bounds[i]) return OVERFLOW;
off+=A.constans[i]*ind;
}
return OK;
}
//赋值
Status Assign(Array &A,ElemType e,...){
va_list ap;
va_start(ap,e);
int off;
if((Locate(A,ap,off))<=0) return ERROR;
A.base[off]=e;
return OK;
}
int Value(Array &A,ElemType e,...){
va_list ap;
va_start(ap,e);
int off;
if((Locate(A,ap,off))<=0) return ERROR;
e=A.base[off];
return e;
}
void print2dim(Array A){
for(int i=0;i<A.bounds[0];i++){
for(int j=0;j<A.bounds[1];j++){
printf("%d ",Value(A,0,i,j));
}
printf("\n");
}
}
//初始化
Status InitArray(Array &A,int dim,...){
if(dim<1||dim>MAX_ARRAY_DIM) return ERROR;
A.dim=dim;
A.bounds=(int*)malloc(dim*sizeof(int));
if(!A.bounds) exit(OVERFLOW);
int elemtotal=1; //元素总长度
va_list ap; //存放变长参数表信息的数组
va_start(ap,dim);
for(int i=0;i<dim;i++){
A.bounds[i]=va_arg(ap,int);
if(A.bounds[i]<0) return ERROR;
elemtotal*=A.bounds[i];
}
va_end(ap);
A.base=(ElemType*)malloc(elemtotal*sizeof(ElemType));
if(!A.base) exit(OVERFLOW);
A.constans=(int*)malloc(dim*sizeof(int));
if(!A.constans) exit(OVERFLOW);
A.constans[dim-1]=1;
for(int i=dim-2;i>=0;i--){
A.constans[i]=A.bounds[i+1]*A.constans[i+1];
}
if(dim==2){ //二维数组初始化
for(int i=0;i<A.bounds[0];i++){
for(int j=0;j<A.bounds[1];j++){
Assign(A,0,i,j);
}
}
}
return OK;
}
int main(){
Array A;
InitArray(A,2,3,4);
Assign(A,3,1,2);
print2dim(A);
system("pause");
}
矩阵压缩
三元组顺序表存储结构:
//稀疏矩阵存储结构
typedef struct{
int i,j; //该非零元的行下表和列下标
ElemType e;
}Triple;
typedef struct{
Triple data[MAXSIZE+1]; //data[0]未用
int mu,nu,tu;
}TSMatrix;
初始化稀疏矩阵:
Status InitMatrix(TSMatrix &M,int m,int n){
M.mu=m;
M.nu=n;
M.tu=1;
return OK;
}
稀疏矩阵插入元素:
Status AddElemM(TSMatrix &M,int ii,int jj,ElemType ee){
M.data[M.tu].i=ii;
M.data[M.tu].j=jj;
M.data[M.tu].e=ee;
M.tu++;
return OK;
}
三元组转换为数组:
Status ConvertM(TSMatrix M,Array &A){
for(int i=1;i<M.tu;i++){
Assign(A,M.data[i].e,M.data[i].i-1,M.data[i].j-1);
}
return OK;
}
矩阵的转置:
for(int col=1;col<=nu;col++)
for(int row=1;row<=mu;row++)
T[col][row]=M[row][col];
算法复杂度为:O(mu X nu)
稀疏矩阵转置:
1.将矩阵的行列数目值相互交换。
2.将每个三元组中的i,j相互调换。
3.重排三元组之间的次序便可实现矩阵的转置。

Status TransposeSMatrix(TSMatrix M,TSMatrix &T){
T.mu=M.nu;
T.nu=M.mu;
T.tu=M.tu;
if(T.tu){
int q=1;
for(int col=1;col<=M.nu;col++){
for(int p=1;p<=M.tu;p++){
if(M.data[p].j==col){
T.data[q].i=M.data[p].j;
T.data[q].j=M.data[p].i;
T.data[q].e=M.data[p].e;
q++;
}
}
}
}
return OK;
}
当tu«mu X nu时,O(mu X tu)小于O(mu X nu);
当tu和mu X nu同数量级,O(mu X tu)大于O(mu X nu).
行逻辑链接顺序表
为了便于随机存取任意一行的非零元,则需要知道每一行的第一个非零元在三元组表中的位置。为此,将指示”行”信息的辅助数组cpot固定在稀疏矩阵的存储结构中,称这种”带行链接信息”的三元组表为行逻辑链接顺序表,其类型描述如下:
typedef struct{
Triple data[MAXSIZE+1]; //非零元三元组表
int rpos[MAXRC+1]; //各行的第一个非零元的位置表
int mu,nu,tu; //矩阵的行数、列数和非零元个数
}RLSMatrix;
十字链表
在十字链表中,每个非零元可用一个含5个域的结点表示,其中i、j和e这3个域分别表示该非零元所在的行、列和非零元的值,向右域right用以链接同一行中下一个非零元,向下域down用以链接同一列中下一个非零元。同一行的非零元通过right域链接成一个线性链表,同一列的非零元通过down域链接称一个线性链表,每个非零元既是某个行链表中的一个结点,又是某个列链表中的一个结点,整个矩阵构成了一个十字交叉链表,故称这样的存储结构为十字链表。可用两个分别存储行链表的头指针和列链表的头指针的一维数组表示之。
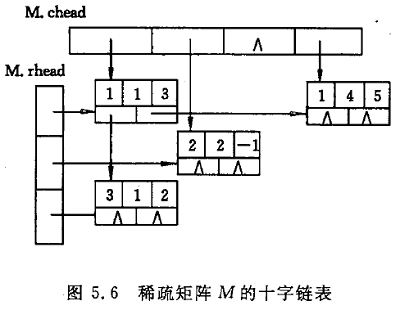
稀疏矩阵的十字链表存储表示:
typedef struct OLNode{
int i,j; //该非零元的行和列下标
ElemType e;
struct OLNode *right,*down; //该非零元所在行表和列表的后继链域
}
typedef struct{
OLink *rhead,*chead; //行和列链表头指针向量基址
int mu,nu,tu;
}CrossList;