线性表的顺序表示指的是用一组地址连续的存储单元依次存储线性表的数据单元。

顺序表的结构
typedef struct{
ElemType *elem;
int length; //顺序表当前的长度
int listsize; //顺序表当前容量
}Sqlist;
数组指针elem表示顺序表的基地址,length表示顺序表的当前长度。listsize表示顺序表当前分配存储的空间大小。
顺序表的初始化
初始化顺序表,并分配内存空间,时间复杂度为O(1)。
Status InitList_Sq(Sqlist& L,int maxsize){
L.elem=(ElemType*)malloc(maxsize*sizeof(ElemType));
if(!L.elem){
exit(OVERFLOW);
}
L.length=0;
L.listsize=maxsize;
return OK;
}
顺序表插入函数实现
在顺序表L指定的位置i插入元素e,首先判断i的合法性,是否在1到L.length+1之间;然后判断顺序表的空间是否已满,已满则追加分配空间;在指定插入元素e,在插入位置之后的元素右移。
Status ListInsert_Sq(Sqlist &L,int i,ElemType e){
if(i<1 || i>L.length+1){
return ERROR; //i值不合法
}
if(L.length>=L.listsize){ //当前存储空间已满 追加空间
ElemType *newbase; //在原有地址上追加空间
newbase=(ElemType*)realloc(L.elem,(L.listsize+LISTINCREMENT)*sizeof(ElemType));
if(!newbase) exit(OVERFLOW);
L.elem=newbase; //新基址
L.listsize+=LISTINCREMENT;
}
ElemType *q=&(L.elem[i-1]); //表示插入的位置
for(ElemType *p=&(L.elem[L.length-1]);p>=q;p--){
*(p+1)=*p; //向后移动
}
*q=e; //插入e
L.length++;
return OK;
}
顺序表删除函数实现
删除顺序表L中指定位置i的元素,首先要判断i的合法性,然后删除元素,同时被删除元素之后的元素左移。
Status ListDelete_Sq(Sqlist &L,int i,ElemType &e){
if((i<1) || (i>L.length+1)) return ERROR;
ElemType *p=&(L.elem[i-1]); //p为被删除元素的位置
e=*p; //读取删除值
ElemType *q=&(L.elem[L.length-1]); //表尾元素的位置
for(p=p+1;p<=q;p++) //被删除元素之后的元素左移
*(p-1)=*p;
L.length--;
return OK;
}
顺序表插入和删除算法时间复杂度分析
当在顺序表存储结构的线性表中某个位置上插入或删除一个数据元素时,其时间主要耗费在移动元素上,而移动元素的个数取决于插入和删除元素的位置。
假设pi是在第i个元素之前插入一个元素的概率,则在长度为n的线性表中插入一个元素时所需移动元素次数的期望值(平均次数)为:
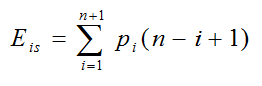
线性表一共存在n+1位置可以插入。
假设qi是删除第i个元素的概率,则在长度为n的线性表中删除一个元素时所需移动元素次数的期望值(平均次数)为:

我们可以假定在顺序表中的任何位置上插入或删除元素都是等概率的,即:
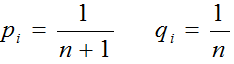
则上述两个式子可以化简为:
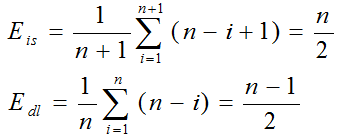
由此可见,在顺序表存储结构的线性表中插入或者删除一个数据元素,平均约移动表中一半元素,如果表长为n,则插入和删除的时间复杂度为O(n).
整体程序
#include <iostream>
#include <stdio.h>
#include <stdlib.h>
#define LISTINCREMENT 10 //追加顺序表的控件大小
//函数结果状态代码
#define OK 1
#define ERROR 0
using namespace std;
typedef int ElemType; //定义数据类型
typedef int Status;
typedef struct{
ElemType *elem;
int length; //顺序表当前的长度
int listsize; //顺序表当前容量
}Sqlist;
//初始化线性表 分配内存空间 时间复杂度为O(1)
Status InitList_Sq(Sqlist& L,int maxsize){
L.elem=(ElemType*)malloc(maxsize*sizeof(ElemType));
if(!L.elem){
exit(OVERFLOW);
}
L.length=0;
L.listsize=maxsize;
return OK;
}
//比较函数
Status compare(ElemType e1,ElemType e2){
if(e1==e2)
return 1;
else
return 0;
}
//定位特定元素在顺序表中的位置
int LocateElem_Sq(Sqlist L,ElemType e,Status (*compare)(ElemType,ElemType)){
for(int i=0;i<L.length;i++){
if(compare(L.elem[i],e)){
return i;
}
}
return 0;
}
//插入元素函数
Status ListInsert_Sq(Sqlist &L,int i,ElemType e){
if(i<1 || i>L.length+1){
return ERROR; //i值不合法
}
if(L.length>=L.listsize){ //当前存储空间已满 追加空间
ElemType *newbase; //在原有地址上追加空间
newbase=(ElemType*)realloc(L.elem,(L.listsize+LISTINCREMENT)*sizeof(ElemType));
if(!newbase) exit(OVERFLOW);
L.elem=newbase; //新基址
L.listsize+=LISTINCREMENT;
}
ElemType *q=&(L.elem[i-1]); //表示插入的位置
for(ElemType *p=&(L.elem[L.length-1]);p>=q;p--){
*(p+1)=*p; //向后移动
}
*q=e; //插入e
L.length++;
return OK;
}
//删除元素
Status ListDelete_Sq(Sqlist &L,int i,ElemType &e){
if((i<1) || (i>L.length+1)) return ERROR;
ElemType *p=&(L.elem[i-1]); //p为被删除元素的位置
e=*p; //读取删除值
ElemType *q=&(L.elem[L.length-1]); //表尾元素的位置
for(p=p+1;p<=q;p++) //被删除元素之后的元素左移
*(p-1)=*p;
L.length--;
return OK;
}
void PrintSqlist(Sqlist L){
for(int i=0;i<L.length;i++)
cout<<L.elem[i]<<" ";
cout<<endl;
}
//合并两个顺序表
void MergeList_Sq(Sqlist La,Sqlist Lb,Sqlist &Lc){
ElemType *pa=La.elem;
ElemType *pb=Lb.elem;
Lc.listsize=Lc.length=La.length+Lb.length;
ElemType *pc=Lc.elem=(ElemType*)malloc(Lc.listsize*sizeof(ElemType));
if(!Lc.elem) exit(OVERFLOW);
ElemType *pa_last=La.elem+La.length-1;
ElemType *pb_last=Lb.elem+Lb.length-1;
while(pa<=pa_last&&pb<=pb_last){ //归并
if(*pa<=*pb) *pc++=*pa++;
else *pc++=*pb++;
}
while(pa<=pa_last) *pc++=*pa++;
while(pb<=pb_last) *pc++=*pb++;
}
int main(){
Sqlist L;
InitList_Sq(L,10);
L.elem[0]=21;
L.elem[1]=18;
L.elem[2]=30;
L.elem[3]=75;
L.elem[4]=42;
L.length=5;
PrintSqlist(L);
ListInsert_Sq(L,3,99);
PrintSqlist(L);
int e;
ListDelete_Sq(L,4,e);
PrintSqlist(L);
system("pause");
}